This is the english version. 
Für die deutsche Version geht es hier entlang.
Framework: Newton's law; Keywords: inverse square law, calculation, differential equation, formula, equations of motion
1) Constant densityNewtonian gravitational Potential V of a thin disc with mass M, radius я and constant surface density ρ=M/π/я², aligned on the z=0-plane:
Polar and equatorial potential with r=0 as a function of z respective with z=0 as a function of r:
Semianalytical solution in terms of elliptic integrals:
Gravitational acceleration vector in the vicinity of the disk:
Equation of motion, vector components:
If there is also a ball with mass Ḿ and radius ʁ in the center, the relevant terms add. Potential of a homogenous sphere:
Here we assume that the ball is permeable and of constant density, so the function for its inner mass is:
Additional components of the acceleration vector in the vicinity of the ball:
The orbit velocity v results from the centrifugal force:
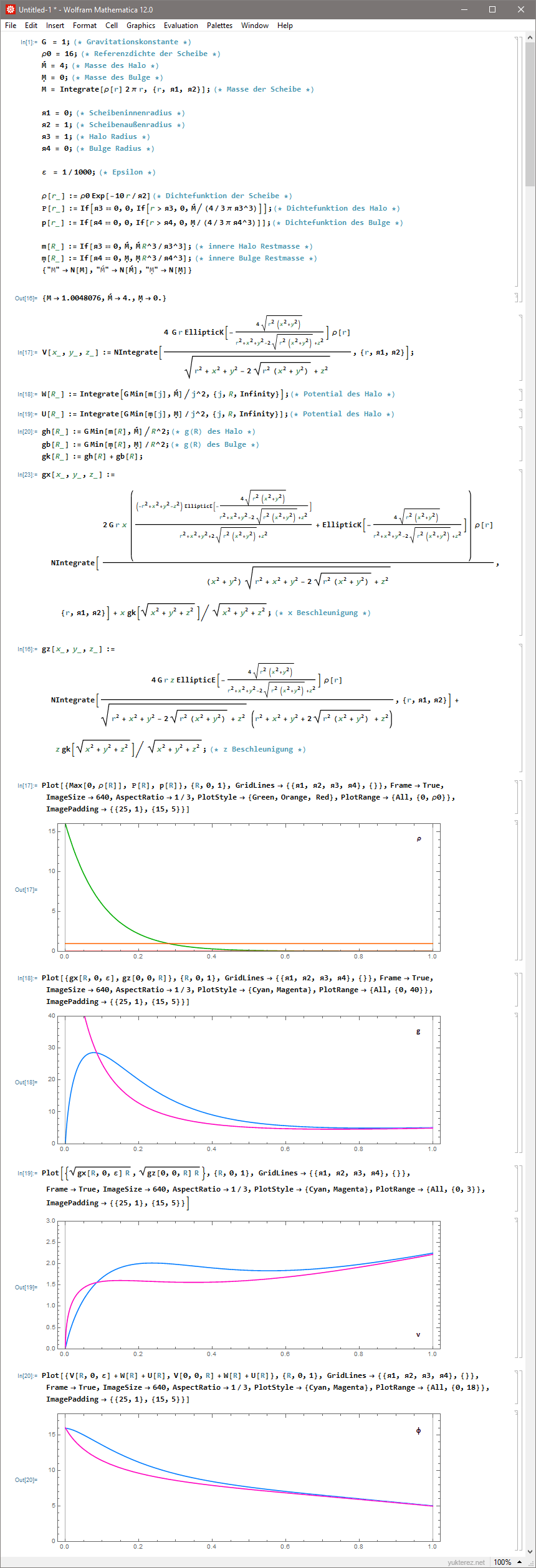
G is the gravitational constant. Required variables:
Definitions of the required functions and elliptical integrals:
For an annular ring with inner and outer radius я1 and я2, a disk with я=я1 is subtracted from a disk with я=я2, respectively the integral from 0 to я is done from я1 to я2 instead. For a comparison of the semianalytic solution with a brute force n-body simulation click here.⑴ Comparison of acceleration g (upper plot), orbit velocity v (middle) and gravitational potential Φ (lower plot); the gray curves show g, v and Φ in the field of a homogenous sphere with Ḿ=ʁ=1, the blue in the field of a disk with M=я=1 at R=x, y=z=0 and the violet at R=z, x=y=0. The horizontal axis is the distance of the test particle to the center, R:
⑵ Plot for the combined field of a saturnoid planet with a central sphere of Ḿ=1, ʁ=я3=10 and a ring with M=1, я1=15, я2=20:
⑶ Sample calculation for an infinite sheet with я=∞, ρ=1 (Solution: g=2πGρ=constant):
⑷ Beside the disk, g is higher than above or below it, while with a sphere or a point mass is is the same in all directions. M=1, R=2:
⑸ Field vectors and contours for different values of constant g in the gravitational field of a disk with M=1, я=20:
⑹ Vector- and contour-plot with an annular disk with M=1, я1=15, я2=20 (obviously the shell-theorem only holds for spheres):
⑺ Vector- and contour-plot with a ring like in the example above plus a spherical mass with Ḿ=1 and ʁ=10 in the center:
Ⅰ Inclined orbit around a thin disk with mass M=1 and radius я=20 (for the initial conditions click on the images):
Ⅱ Another inclined orbit around the same disk as above:
Ⅲ Closed polar orbit around the same disk as above:
Ⅳ Polar orbit around a sphere with Ḿ=1, ʁ=я3=10 with an annular ring of mass M=1/2 and an inner/outer-radius of я1=15, я2=20:
Ⅴ Closed polar orbit around a ring planet with the same properties as above:
Ⅵ Circular equatorial orbit, sphere and ring with the same properties as in the previous example:
Ⅶ Inclined orbit, sphere: Ḿ=1/2, ʁ=я3=10, ring: M=1, я1=15, я2=20:
Ⅷ Gravity tunnel through a saturnoid and permeable planet with Ḿ=1, ʁ=10 with a ring of mass M=1/2:
Ⅸ Gravity tunnel through a ring with M=1:
Ⅹ Gravity tunnel with inclination, ring like in the last example:
Ⅺ Star-shaped orbit around an annular ring with M=1, я1=15, я2=20:
Ⅻ Orbit inside a permeable disk of M=1, я=20 (z=0+ε, z"=0), Initial velocity v⊥=√(GM/я):
Display, columns [1|2|3|4]→[position|velocity|acceleration|distribution]
Video in Full HD: click here. To view the full code click here, and here for an other example.
Remarks: - To reduce the CPU time, the integral for V can be changed from ∫{...}d[θ=0..2π] to 2∫{...}d[θ=0..π] due to the symmetry of the disk if the density function is isotrope. With constant density the semianalytical solution is recommended, since it is significantly faster than the purely numerical integral.
- Plot ⑴ shows that the circular orbit velocity inside a homogenous disk grows stronger with increasing radius than it would inside a homogenous sphere. In row 2 the blue v-curve for R=r, z=0 shows the circular orbit velocity in the equatorial plane, while the violet v-curve shows the required horizontal velocity for z"=0 (due to the asymmetry of the body and it's field, at low heights above the disk's center closed polar orbits are not always possible).
- In plot ⑵ g diverges on the inner and outer edges of the annular disk; so to say, the disk gets squeezed into a ring. This is one of the reasons why protoplanetary disks can collapse into planets. The divergence on the exact edges can be avoided by keeping a minimum distance on the scale of the mean distance between the particles that form the disk, so the test particle does not plunge onto the infinitely thin disk with finite area-density, but infinite volume-density. To study orbits in the purely equatorial plane that reach into the disk, one sets z'=z"=0, z=0+ε whereby ε in the context of a galaxy would be the mean distance between the stars, or in the context of saturn's rings the radius of the particles that form the annular disk.
- The 2nd line in Plot ⑸ draws the surfaces of constant gravity which define the sea level if the disk was covered with water and the water's mass was small compared to the mass of the disk.
