
 This is the english version.
This is the english version.  Eine deutschspachige Version findet sich hier
Eine deutschspachige Version findet sich hier
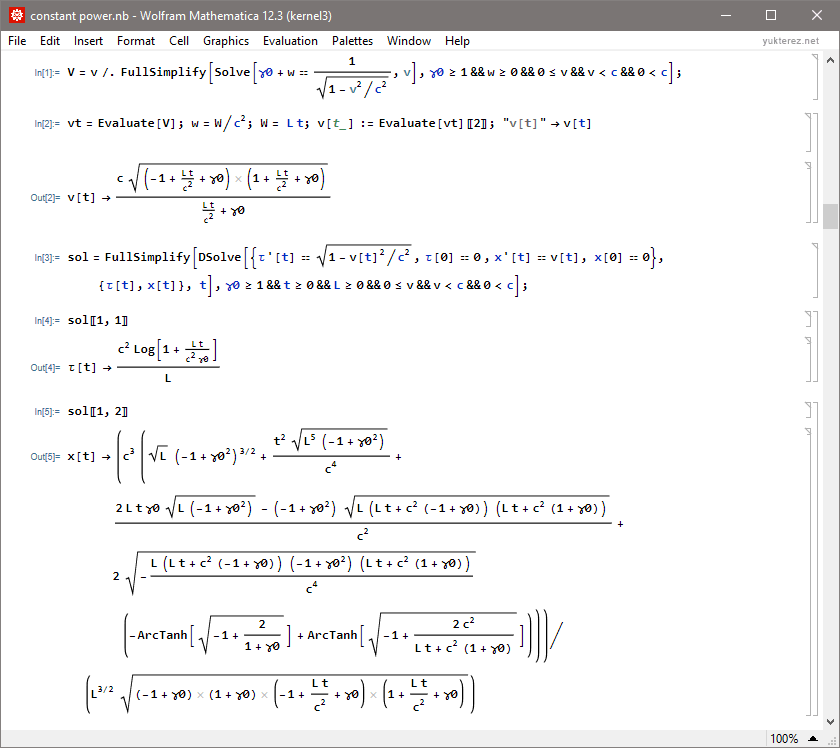
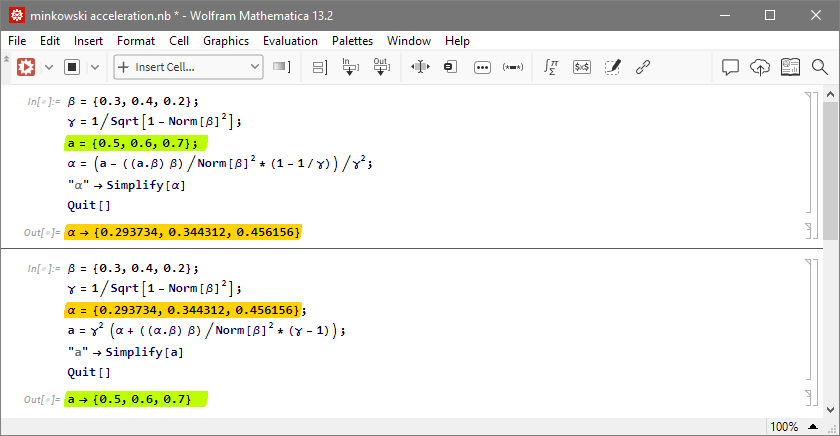
Index: constant force | constant coordinate acceleration | constant power, discussion (autotranslate from german): click here

 This is the english version.
This is the english version.  Eine deutschspachige Version findet sich hier
Eine deutschspachige Version findet sich hier







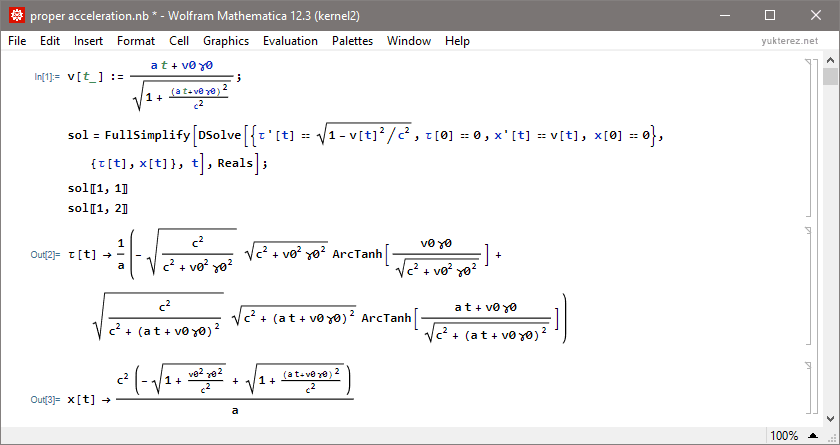




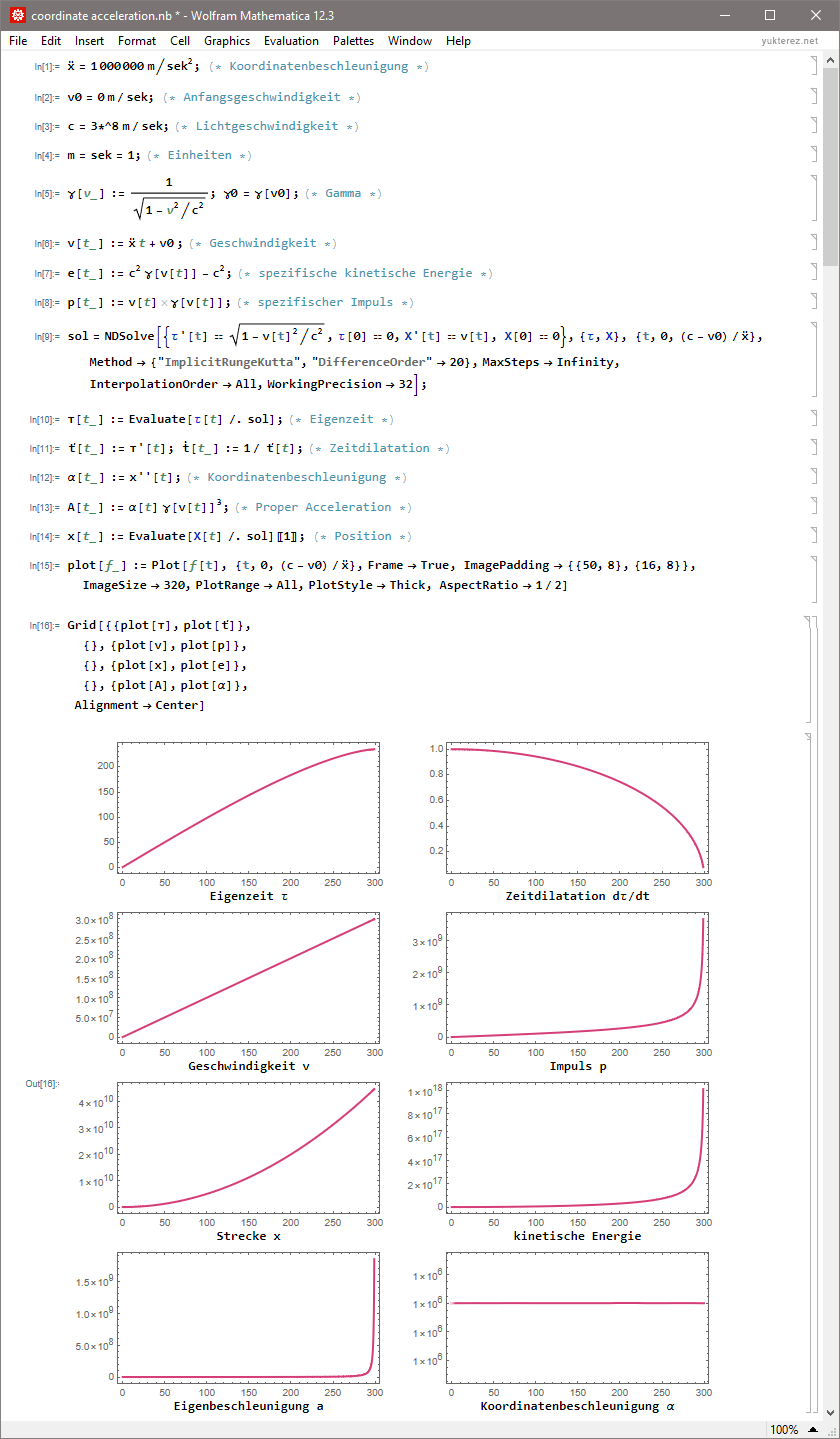
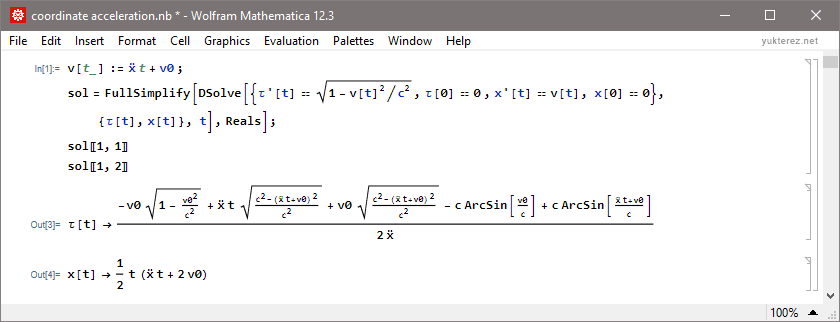





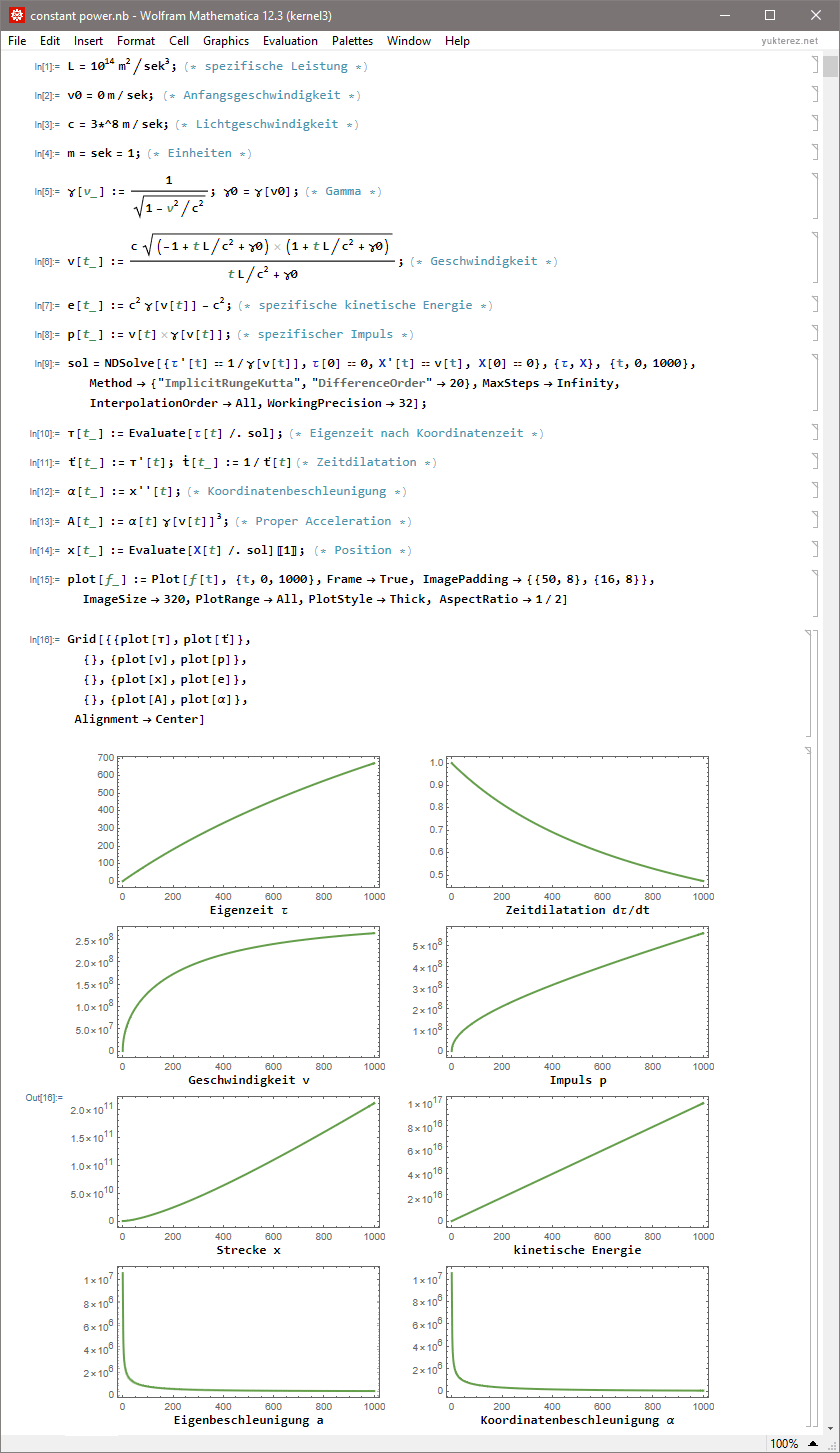


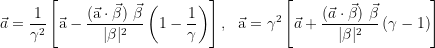


Mitglieder in diesem Forum: 0 Mitglieder und 5 Gäste