Schwarzloch Interior
Verfasst: Do 19. Okt 2017, 07:19




Gemeinsame Komponenten:
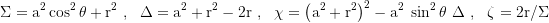

Boyer-Lindquist Koordinaten:
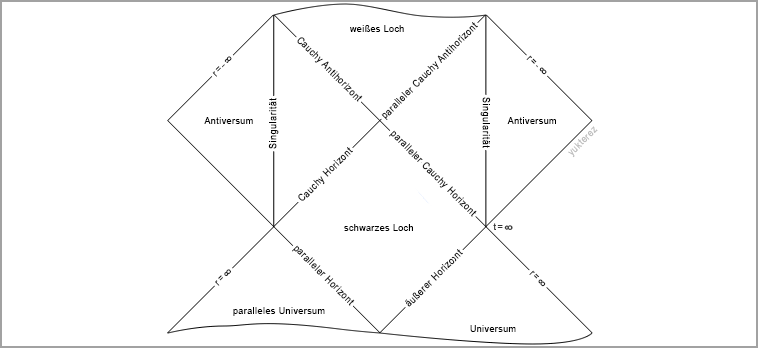
Diese Koordinaten stellen, ähnlich wie Droste Koordinaten (auf die sie sich mit a=0 reduzieren), das Geschehen im Bezugssystem eines feldfreien Beobachters dar. Die Zeitdilatation wird am äußeren Horizont unendlich, alle einfallenden Objekte frieren dort ein und korotieren mit stehengebliebenen Uhren unendlich oft mit dem schwarzen Loch mit. Die Trajektorien von neutralen mit der Freifallgeschwindigkeit aus der Unendlichkeit einfallenden oder mit der radialen Fluchtgeschwindigkeit davonfliegenden Partikeln haben in diesen Koordinaten ein konstantes θ. Der lokale Referenzbeobachter relativ zu dem die kinetische Energie und Dreiergeschwindigkeit eines Testpartikels bestimmt wird ist ein ZAMO auf der Position des Testpartikels.
Sortierung:

Metrischer Tensor:

statisches Limit:

Kartesische Einbettung:
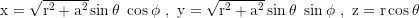

Kerr-Schild Koordinaten:
Die Koordinatenzeit und der Azimutalwinkel werden über drehimpulsfrei einfallende Lichtstrahlen die die Zeit und den Winkel ihres Schalendurchgangs encodiert haben synchronsiert um die Unendlichkeiten die in Buchhalterkoordinaten am Horizont auftreten zu eliminieren. Mit der geglätteten Zeitachse legen polar einfallende Lichtrahlen pro GM/c³ Koordinatenzeit ein GM/c² Koordinatenstrecke zurück. Wie in erweiterten Finkelstein Koordinaten, auf die sie sich mit a=0 reduzieren, können Trajektorien in diesen Koordinaten auch duch in die Horizonte hindurch gerechnet werden.
Sortierung:

Metrischer Tensor:
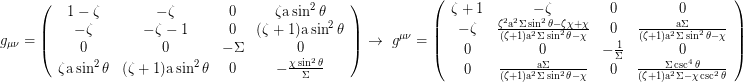
statisches Limit:

Kartesische Einbettung:


Übersetzung:


Gemeinsamkeiten:
Photonenorbits und andere Bahnen mit kontantem r stellen sich in beiden Koordinatenssystemen gleich dar (wenn dr=0 ergibt sich dt̄=dt und dφ̄=dФ). Die Polwinkel von drehimpulsfreien und aus dem Unendlichen einfallenden Freifallern (Raindrops) bleiben ebenfalls in beiden Koordinatensystemen konstant, allerdings nur in der pseudosphärischen r,θ,φ-Darstellung und nicht in der kartesischen x,y,z-Einbettung (siehe hier für einen Vergleich r,θ,φ vs x,y,z).

Farbcode, Horizonte:
In den folgenden Beispielen werden Freifaller (lokale radiale Fallgeschwindigkeit gleich der negativen Fluchtgeschwindigkeit, Epot=-Ekin, L=0, θ=konstant) und Photonen (lokale Radialgeschwindigkeit konstant c) aus verschiedenen Richtungen direkt auf ein schwarzes Loch (a=0.998) geschossen, und deren Bahnanimationen und Weltlinienplots in beiden Systemen verglichen. Die Rotation des schwarzen Lochs läuft auf der x,y-Projektion (rechts) gegen den Uhrzeigersinn. Farbcode wie hier:


Animationsdisplay:
- 1. Spalte: τ propr = Eigenzeit, t coord = Koordinatenzeit eines feldfreien Beobachters, т coord = finkelsteinartige Kerr-Schild Koordinatenzeit, affineP = affiner Parameter (bei Photonen anstatt der Eigenzeit), γ total = insgesamte Zeitdilatation relativ zum feldfreien Beobachter (innerhalb des Ereignishorizonts ohne physikalische Bedeutung), ς gravt = gravitative Zeitdilatation, Lapse Funktion (innerhalb von r+ wie γ), r coord = r Koordinate, φ longd = Azimutwinkel, je nach Koordinaten entweder φ̄ oder Ф, θ lattd = pseudosphärischer Polarwinkel
- 2. Spalte: M irred = irreduzible Masse, Ř cic.φ = azimutaler Gyrationsradius, Σ crc.θ = polarer Gyrationsradius, E kinet = kinetische Energie relativ zum auf fixer r-Koordinate schwebenden ZAMO, E poten = potentielle Energie, E total = Gesamtenergie des Testpartikels, CarterQ = Carter Konstante, a SpinP = Spinparameter
- 3. Spalte: L axial = azimutaler Drehimpuls, L polar = polarer Drehimpuls, α dv/dτ = Beschleunigung im System des Testpartikels, R carts = kartesischer Radius, xyz carts = kartesische Koordinaten, s dstnc = aufintegrierte Strecke
- 4. Spalte: ω fdrag = Frame Dragging Winkelgeschwindigkeit dφ/dt, v fdrag = Geschwindigkeit mit der ein Partikel vor Ort retrograd fliegen müsste um relativ zu einem feldfreien Beobachter stationär zu bleiben bzw. Korotationsgeschwindigkeit eines lokal drehimpulsfreien ZAMO (innerhalb der Ergosphäre größer als c), Ω fdrag = auf kartesische Hintergrundkoordinaten projizierte Frame Dragging Geschwindigkeit, v propr = Proper Velocity (Rapidität), v obsvd = beobachtete Geschwindigkeit, v escape = Fluchtgeschwindigkeit (innerhalb von r+ ohne direkte physikalische Bedeutung), v delay = beobachtete Geschwindigkeit abzüglich der Frame Dragging Komponente, v local = lokale Geschwindigkeit relativ zu einem ZAMO

Beispiele (beide Koordinatensysteme in kartesischer Projektion): siehe unten