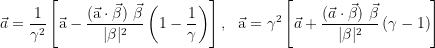Seite 1 von 1
Relativistische Beschleunigung
Verfasst: Mi 23. Jun 2021, 03:34
von Yukterez
Das ist die deutschsprachige Version.
An english version is available on
en.yukterez.net Inhalt:
konstante Kraft |
konstante Koordinatenbeschleunigung |
konstante Leistung , Diskussion:
hier entlang
Relativistische Beschleunigung
Verfasst: Mi 23. Jun 2021, 03:38
von Yukterez
KONSTANTE KRAFT
Die Geschwindigkeit v ergibt sich über den Gammafaktor γ
mit dem relativistischen Impuls p
wobei Kraft F, Ruhemasse m und Eigenbeschleunigung a über
mit dem Differential von Impuls p über Koordinatenzeit t verknüpft sind. Damit ergibt sich mit F=konstant
Plot mit der Koordinatenzeit t als x-Achse (SI-Einheiten, Impuls und Energie als spezifische Größen pro kg Ruhemasse):
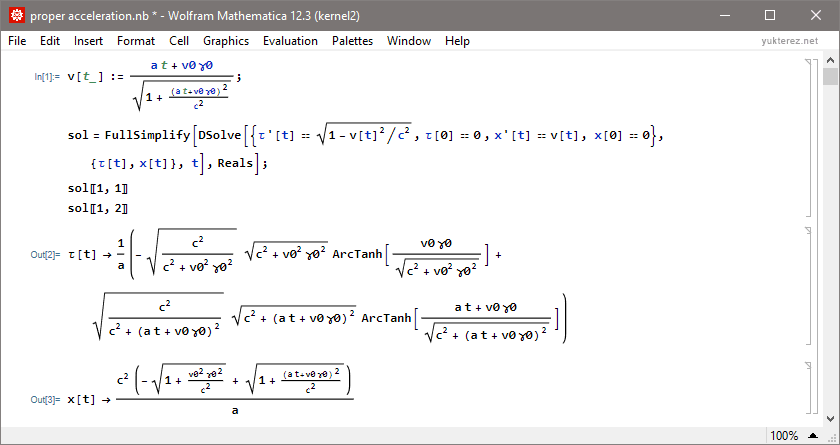
Analytische Lösungen für Eigenzeit τ und Strecke x:
Code:
Code: Alles auswählen
(* Eigenbeschleunigung, Methode 1 *) Code: Alles auswählen
(* Eigenbeschleunigung, Methode 2 *) Code: Alles auswählen
(* Eigenbeschleunigung, Methode 3 *) 3 verschiedene Methoden um ans Ziel zu kommen:
hier entlang
Relativistische Beschleunigung
Verfasst: Mi 23. Jun 2021, 03:46
von Yukterez
KONSTANTE KOORDINATENBESCHLEUNIGUNG
Mit α=dv/dt=d²x/dt²=a/γ³=konstant ist die Formel für die Geschwindigkeit v ganz einfach
Die Lichtgeschwindigkeit wäre bei konstanter Koordinatenbeschleunigung erreicht wenn
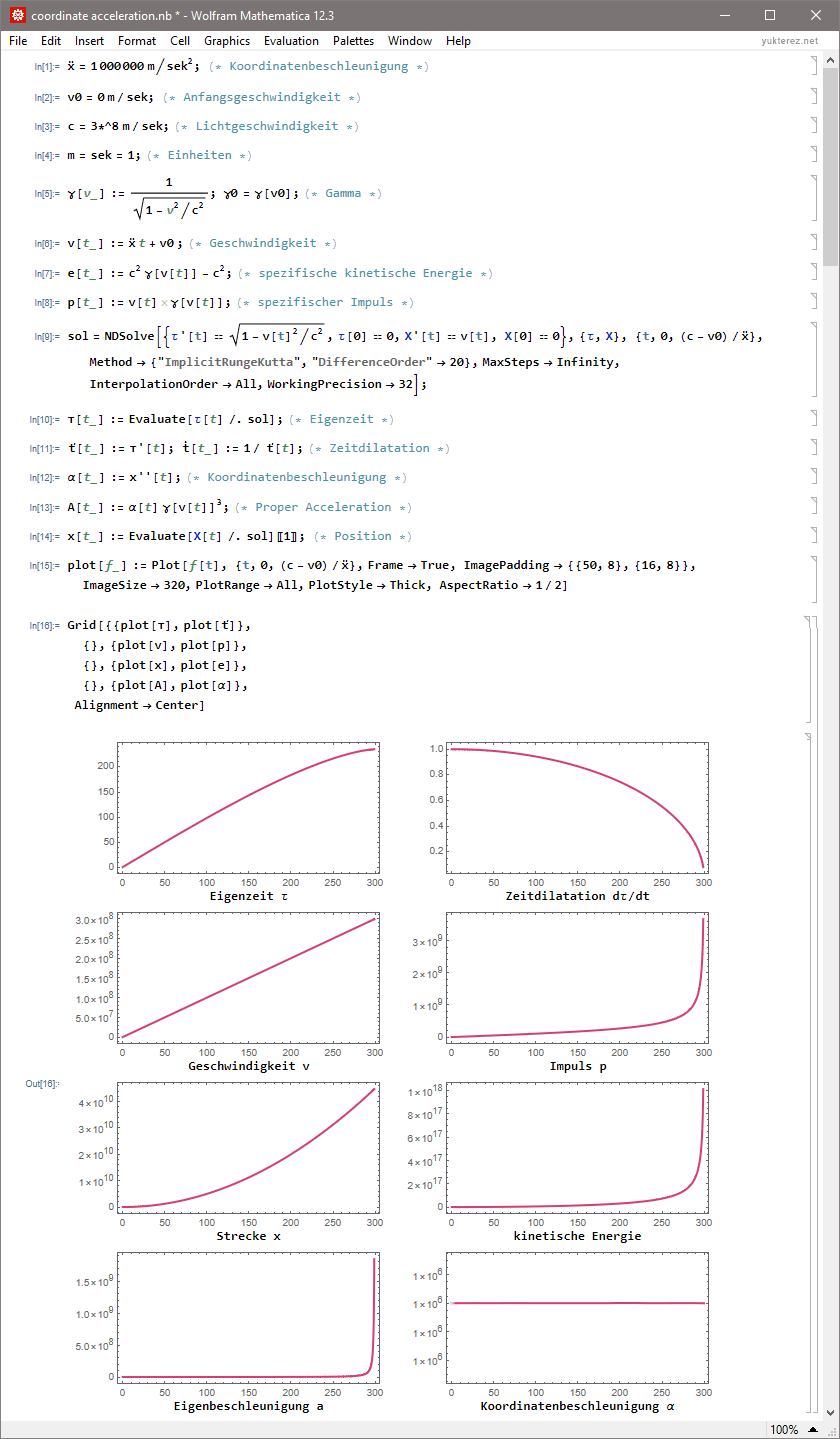
Plot mit der Koordinatenzeit t als x-Achse (SI-Einheiten, Impuls und Energie als spezifische Größen pro kg Ruhemasse):
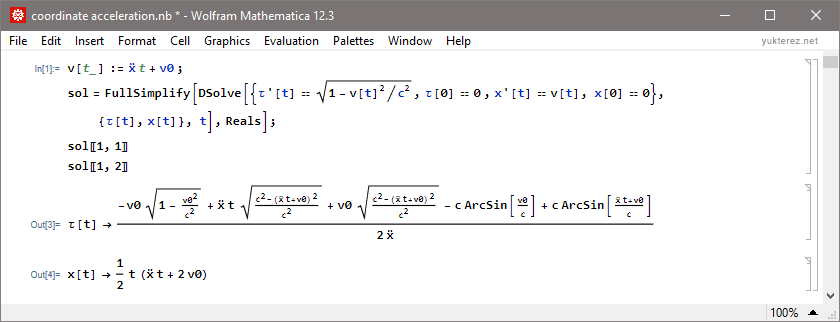
Analytische Lösungen für Eigenzeit τ und Strecke x:
Code:
Code: Alles auswählen
(* konstante Koordinatenbeschleunigung ẍ *)
Relativistische Beschleunigung
Verfasst: Mi 23. Jun 2021, 03:58
von Yukterez
KONSTANTE LEISTUNG
Bei konstanter Leistung L nimmt die Energie mc²γ linear mit t zu. Daher gilt
mit der hineingesteckten Arbeit W
Nach v aufgelöst ergibt das
Plot mit der Koordinatenzeit t als x-Achse (SI-Einheiten, Impuls und Energie als spezifische Größen pro kg Ruhemasse):
Analytische Lösungen für Eigenzeit τ und Strecke x:
Code:
Code: Alles auswählen
(* konstante Leistung *)
Relativistische Beschleunigung
Verfasst: Mi 12. Feb 2025, 20:43
von Yukterez
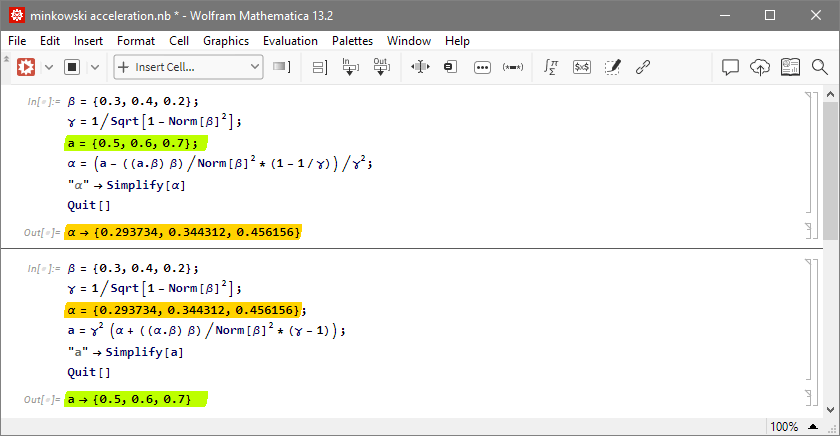
Vektor Notation: α ist die Koordinatenbeschleunigung des beschleunigten Beobachters im System des unbeschleunigten Beobachters, a ist die Eigenbeschleunigung des beschleunigten Beobachters in seinem eigenen System, v=βc ist ihre Relativgeschwindigkeit während sie aneinander vorbeifliegen:
Code:
Code: Alles auswählen
β={vx/c,vy/c,vz/c};Code: Alles auswählen
β={vx/c,vy/c,vz/c};Anwendung im Kontext der Schwarzschild Metrik:
physics.stackexchange.com/a/842494

 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  An english version is available on en.yukterez.net
An english version is available on en.yukterez.net