Notizblock

In dieser Serie wird die Perspektive eines Beobachters der aus dem Unendlichen mit der negativen Fluchtgeschwindigkeit
auf ein mit a=0.7 rotierendes und ℧=0.7 geladenes SL zufällt gezeigt und mit der eines radial stationären Beobachers im lokalen
LNRF verglichen. Das schwarze Loch hat eine mit der lokalen Kreisbahngeschwindigkeit rotierende Akkretionsscheibe mit einen
Innenradius von rᵢ=ISCO=1.63678 und einem Außenradius von rₐ=7; das numerische Display wird gefolgt von geraytracten Bildern:



Der erste Teil zeigt die Szene mit Akkretionsscheibe, und der zweite ohne. Im dritten Teil befindet sich eine mit der Frame
Dragging Geschwindigkeit korotierende Schale die ein halbdurchsichtiges Bild der Erdoberfläche abstrahlt knapp über dem
äußeren Ereignishorizont auf 1.0001r₊, siehe links in kartesischen x,y,z und rechts in pseudosphärischen r,θ,φ Koordinaten:



In der kartesischen Darstellung ist zu sehen dass die Singularität ein Ring mit dem physikalischen Radius R=a ist, während
sie in der pseudosphärischen Darstellung bei r=0 dargestellt ist. Der kartesische Radius R und Breitengrad Θ stehen mit den
pseudosphärischen Koordinaten r,θ,φ im Verhältnis R=√(r²+a² Sin[θ]), Θ=ArcCos[(r Cos[θ])/√(r²+a² Sin[θ]²)], Φ=φ.
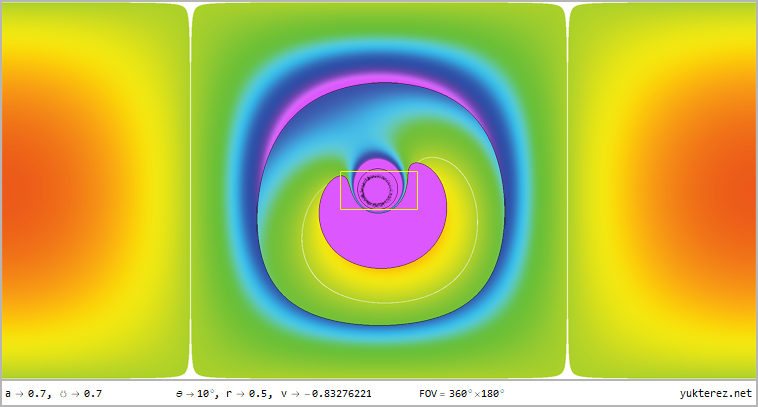
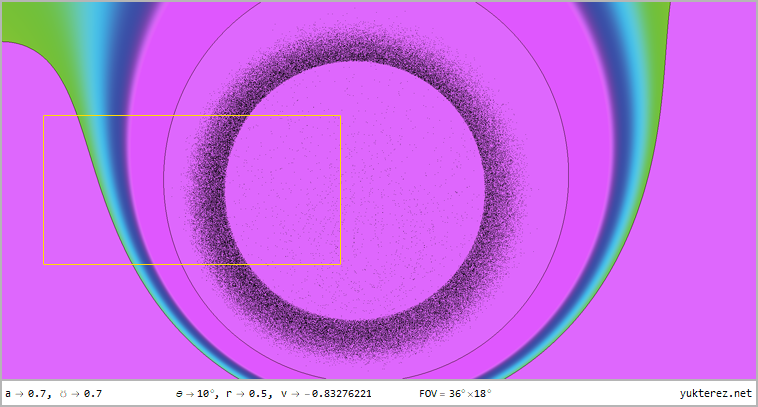
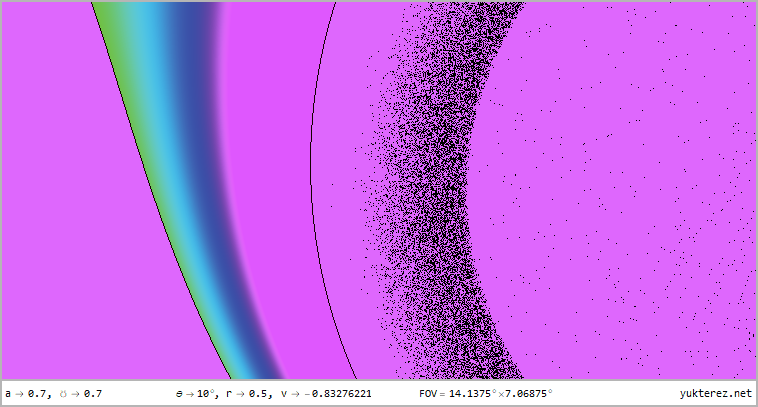
Ein Freifaller aus dem Unendlichen (E=1) hat konstantes θ und φ (jedoch kein konstantes Θ). Der vierte Teil zeigt die
Frequenzverschiebung des Milchstraßenhintergrunds und der Akkretionsscheibe, Farbcodierung im Bereich von
fe/f0=0..2 (weiß für fe/f0=1):



In der ZAMO Perspektive befindet sich der Beobachter nicht am Horizont, sondern knapp über dem äußeren bzw. unter dem
inneren Horizont wo die Flucht- bzw. Freifallgeschwindigkeit (also die Relativgeschwindigkeit zum Raindrop) v=0.9999c beträgt.
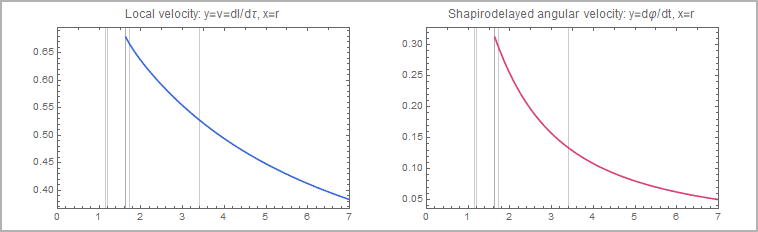
Rotationsprofil der Akkretionsscheibe: lokale Kreisbahngeschwindigkeit relativ zu einem ZAMO und shapiroverzögerte
Winkelgeschwindigkeit als Funktion von r (die Scheibe rotiert gegen den Uhrzeigersinn, also von links auf den Beobachter zu):



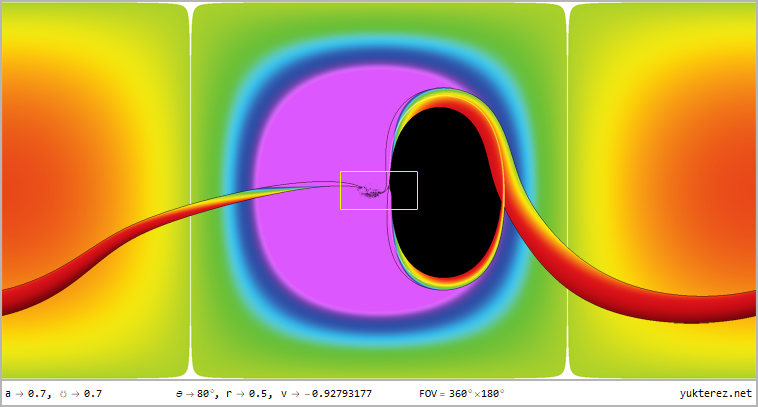
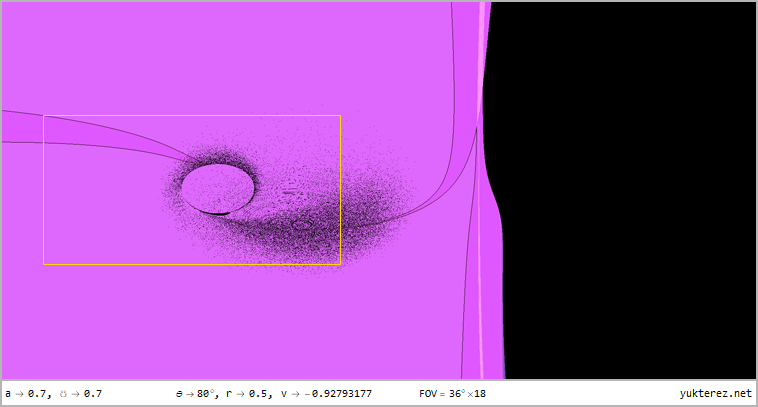
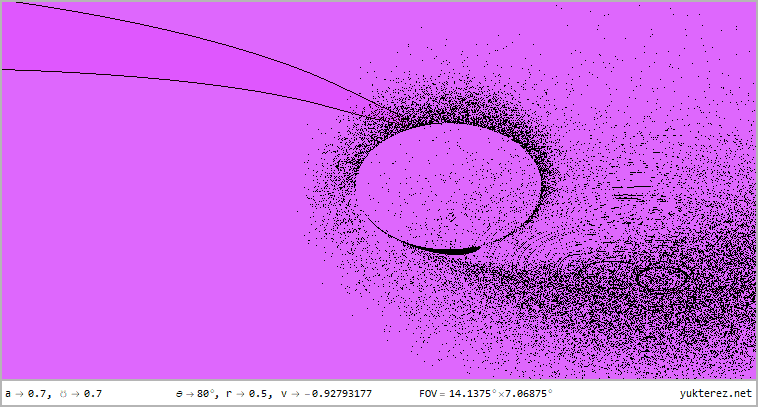
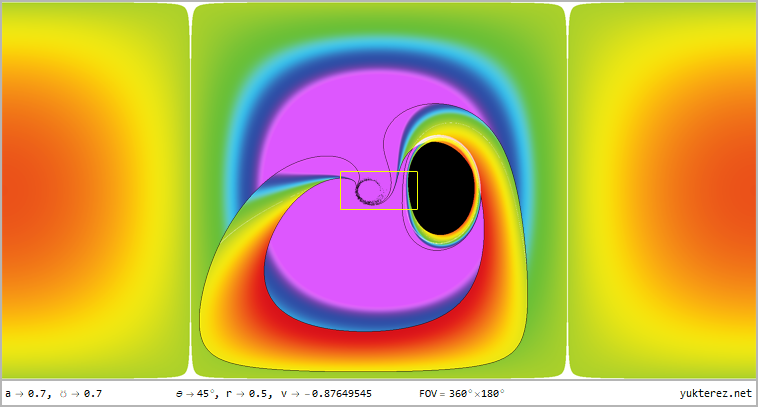
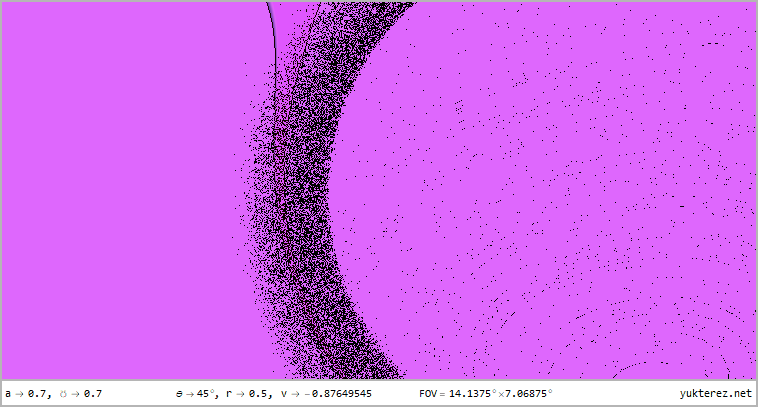
Gezeigt wird die Perspektive auf r=12, r=4, r=r₊, r=r₋ & r=0.5 für Latituden von θ=80°, θ=45° & θ=10° im 360°×180° Voll-
panorama im Plattkartenformat und als stereografische Projektion mit dem vorderen und hinteren Sichtfeld; das einleitende
numerische Display zeigt die Geschwindigkeit relativ zu einem lokalen ZAMO (an den Horizonten ist der einzig mögliche ZAMO ein
bahndrehimpulsfreies Photon, daher ist bei r₊ und r₋ die lokale Geschwindigkeit v=c):

r=12, θ=80°  →  R=12.01979, Θ=80.01663°











r=4, θ=80°  →  R=4.058968, Θ=80.14674°











r=r₊=1.141421 (äußerer Ereignishorizont), θ=80°  →  R=1.333442, Θ=81.45175°











r=r₋=0.858579 (innerer Cauchyhorizont), θ=80°  →  R=1.101082, Θ=82.21803°











r=0.5, θ=80°  →  R=0.851601, Θ=84.14830°

r=12, θ=80°  →  R=12.01979, Θ=80.01663°











r=4, θ=80°  →  R=4.058968, Θ=80.14674°











r=1.143138 (knapp über dem äußeren Horizont), θ=80°  →  R=1.334912, Θ=81.448296°











r=0.857171 (knapp unter dem inneren Horizont), θ=80°  →  R=1.099985, Θ=82.223075°











r=0.5, θ=80°  →  R=0.851601, Θ=84.14830°

r=12, θ=45°  →  R=12.01020, Θ=45.04866°











r=4, θ=45°  →  R=4.030509, Θ=45.43207°











r=r₊=1.141421 (äußerer Ereignishorizont), θ=45°  →  R=1.244123, Θ=49.55368°











r=r₋=0.858579 (innerer Cauchyhorizont), θ=45°  →  R=0.991039, Θ=52.22251°











r=0.5, θ=45°  →  R=0.703562, Θ=59.83321°

r=12, θ=45°  →  R=12.01020, Θ=45.04866°











r=4, θ=45°  →  R=4.030509, Θ=45.43207°











r=1.1428844 (knapp über dem äußeren Horizont), θ=45°  →  R=1.2454656, Θ=49.543783°











r=0.8574999 (knapp unter dem inneren Horizont), θ=45°  →  R=0.990104, Θ=52.236446°











r=0.5, θ=45°  →  R=0.703562, Θ=59.83321°

r=12, θ=10°  →  R=12.00062, Θ=10.01665°











r=4, θ=10°  →  R=4.001847, Θ=10.14883°











r=r₊=1.141421 (äußerer Ereignishorizont), θ=10°  →  R=1.147875, Θ=11.68651°











r=r₋=0.858579 (innerer Cauchyhorizont), θ=10°  →  R=0.867141, Θ=12.81686°











r=0.5, θ=10°  →  R=0.514563, Θ=16.87593°

r=12, θ=10°  →  R=12.00062, Θ=10.01665°











r=4, θ=10°  →  R=4.001847, Θ=10.14883°











r=1.1426959 (knapp über dem äußeren Horizont), θ=10°  →  R=1.1491428, Θ=11.683043°











r=0.857704 (knapp unter dem inneren Horizont), θ=10°  →  R=0.8662746, Θ=12.821906°











r=0.5, θ=10°  →  R=0.514563, Θ=16.87593°

Das schwarze Rauschen das im inneren Horizonts beobachtet wird ist numerisch und tritt um die Singularität herum auf. Zoom:





















Innerhalb des Rings befindet sich das Fenster in den negativen Raum (Antiversum), welcher sofern dieser nicht nur ein
mathematisches Artefakt ist in der Realität vermutlich leer ist. In den Bildern auf dieser Seite wird ein Spiegel zwischen dem
Ring aufgespannt, aber im Grunde ist es unbekannt was man an dieser Stelle sehen würde, da unklar ist ob die Region innerhalb
des Cauchyhorizonts überhaupt als physikalisch betrachtet werden darf.

Unverzerrte Ansicht der Akkretionsscheibe und Flächen des schwarzen Lochs aus einem Blickwinkel von Θ=80°:



Das sähe ein Beobacher wenn die Flächen und der Ring des SL sichtbar wären und weder Gravitationslinseneffekt noch
Frequenzverschiebung aufträte. Der BL Innen/Außenradius der Akkretionsscheibe rᵢ=1.63678, rₐ=7 projiziert mit Rᵢ=1.780184,
Rₐ= 7.034913 in den kartesischen flachen Raum. Der äußere Horizont befindet sich bei r₊=1.1414214 → R₊=1.3389708 und
die Ringsingularität bei rᵣ=0 → Rᵣ=a=0.7

In diesen Bildern wurde der Sternenhintergrund bei rₛₚₕ=500 (in natürlichen Einheiten von G=M=c=k=1) aufgespannt, der
Integrationsbereich für den affinen Parameter des Photons läuft von 0 bis tᵢ=-100rₛₚₕ. Wenn die Schrittweite der Integration
kleiner als 10⁻⁵ oder die gesetze Grenze für den affinen Parameter erreicht wird bricht die Integration ab und der betroffene
Pixel wird schwarz dargestellt.

Die verwendeten Koordinaten sind Raindrop Doran Koordinaten (für mehr Details siehe hier). Außerhalb des Horizonts empfehlen
sich Boyer Lindquist Koordinaten da der BL Code weniger Rechenzeit und Arbeitsspeicher benötigt. In beiden Fällen erfolgt die
Ausgabe im Plattkartenformat und kann mit kartographie.yukterez.net in andere Formate umgerechnet werden, so wie
beispielsweise in die stereografische Projektion.

Innerhalb des Horizonts müssen auch für die ZAMO Perspektive Raindrop oder Kerr Schild Koordinaten verwendet werden, die
Umrechnung der lokalen Geschwindigkeit vom einen System ins andere findet sich hier (v=0 in Raindrop Koordinaten bedeutet
freier Fall aus der Unendlichkeit, und v=0 in BL Koordinaten das System eines ZAMO). Im numerischen Display ist die lokale
Geschwindigkeit relativ zu einem ZAMO angegeben.

Die Feldgleichungen und diverse Koordinatensysteme finden sich auf geodesics.yukterez.net, der Code für den Simulator auf
kerr.newman.yukterez.net und der relativistische Raytracer auf raytracing.yukterez.net; für den Fall in ein nichtrotierendes
und ungeladenes SL ohne Scheibe siehe schwarzschild.yukterez.net

Alternatives Layout mit der Freifaller Perspektive in der linken Spalte und der ZAMO Perspektive in der rechten: hier entlang