Notizblock

Critical value for the dark energy ΩΛ in a closed universe; a smaller value leads to a big crunch, the exact value brings the expansion to a halt and a larger value leads to eternal accelerated expansion since then the Hubbleparameter never reaches 0 but converges to a constant value:


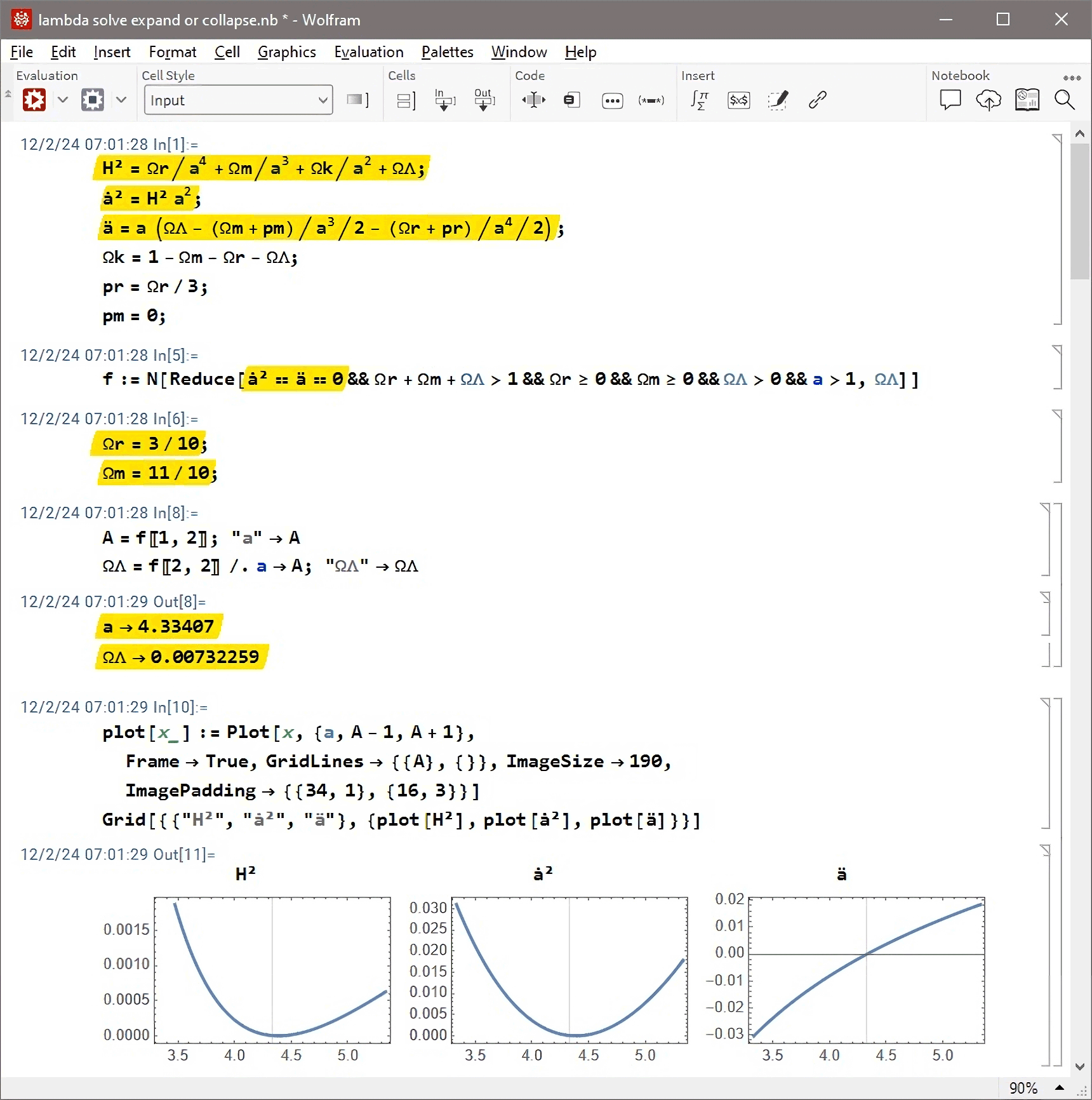
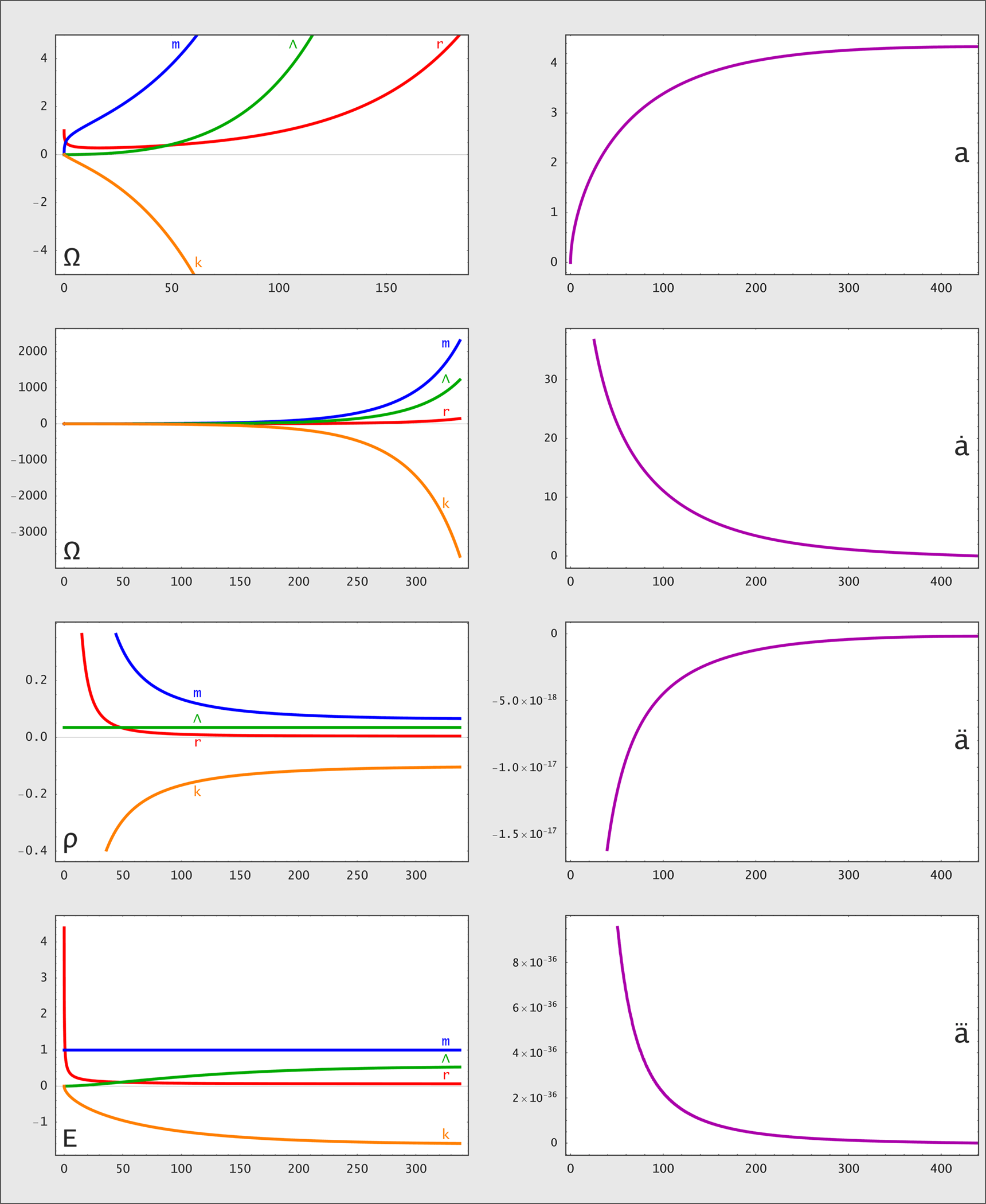
Example: at In[1] we define the normalized Hubbleparameter H and the first and second time derivatives (ȧ and ä) of the normalized scalefactor as well as the relations between pressure, density and curvature. At In[5] the velocity and acceleration of the expansion are set to 0 to solve for the limit between expansion and contraction. At In[6] we choose our values for the matter Ωm and radiation Ωr. At In/Out[8] we evaluate the required dark energy ΩΛ and the scalefactor a when the equilibrium occurs and plot the functions at Out[11]. The plot values right of the vertical gridline belong to such values of a which are reached at no predictable time t since at the maximal value of a, here a=4.33407, we get H=0 and dH/dt=0, which is an unstable equilibrium:



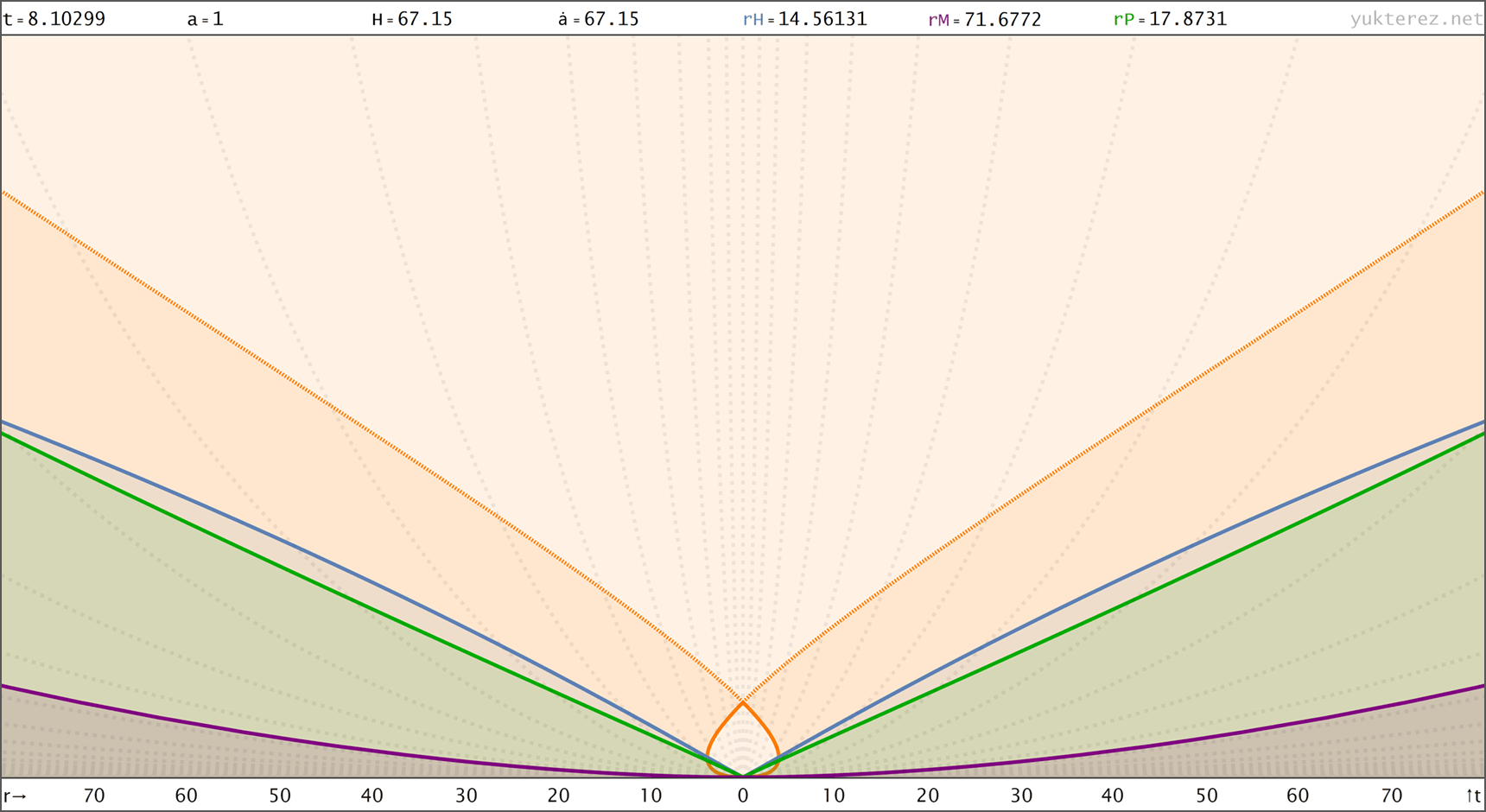
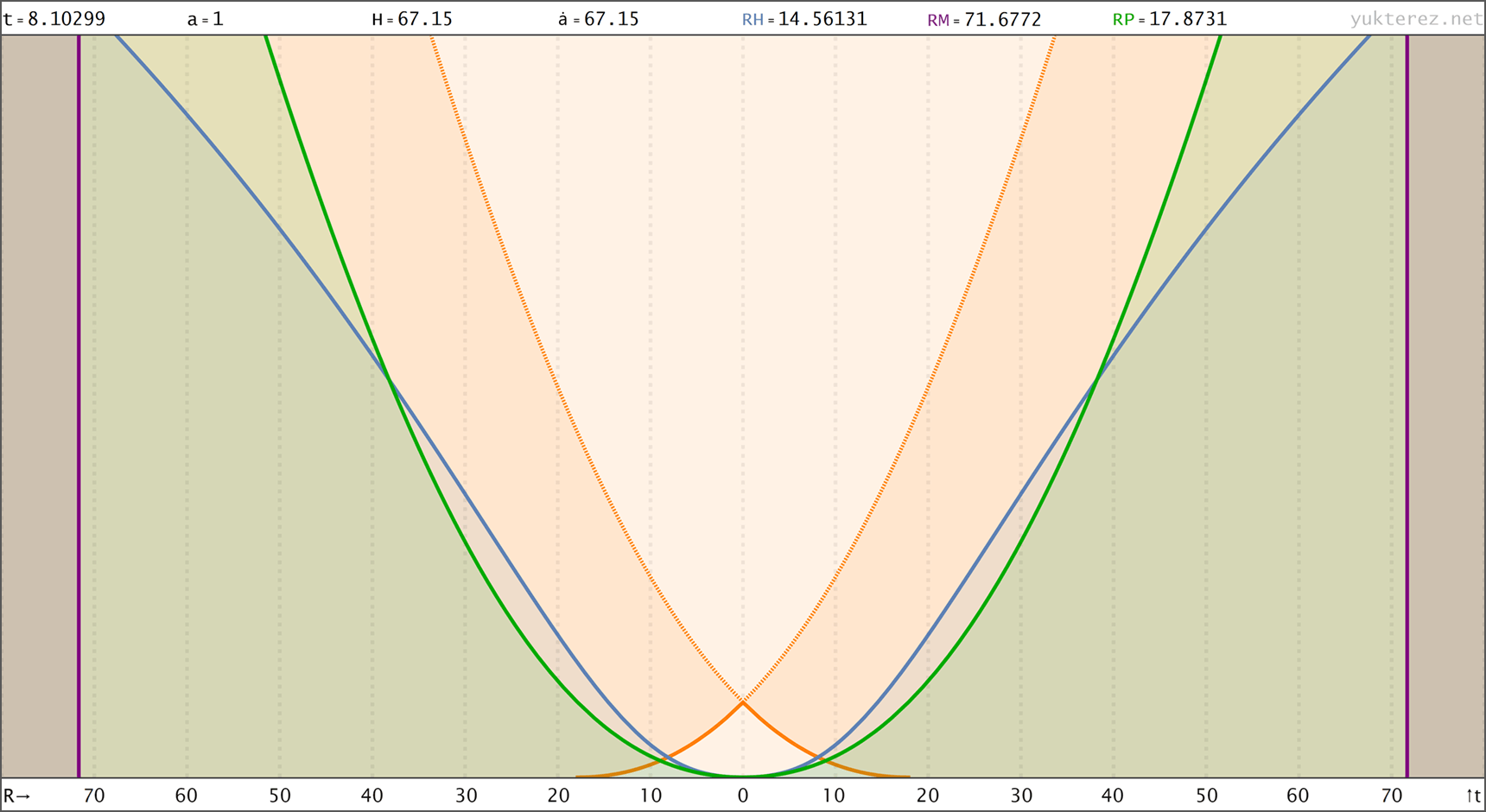
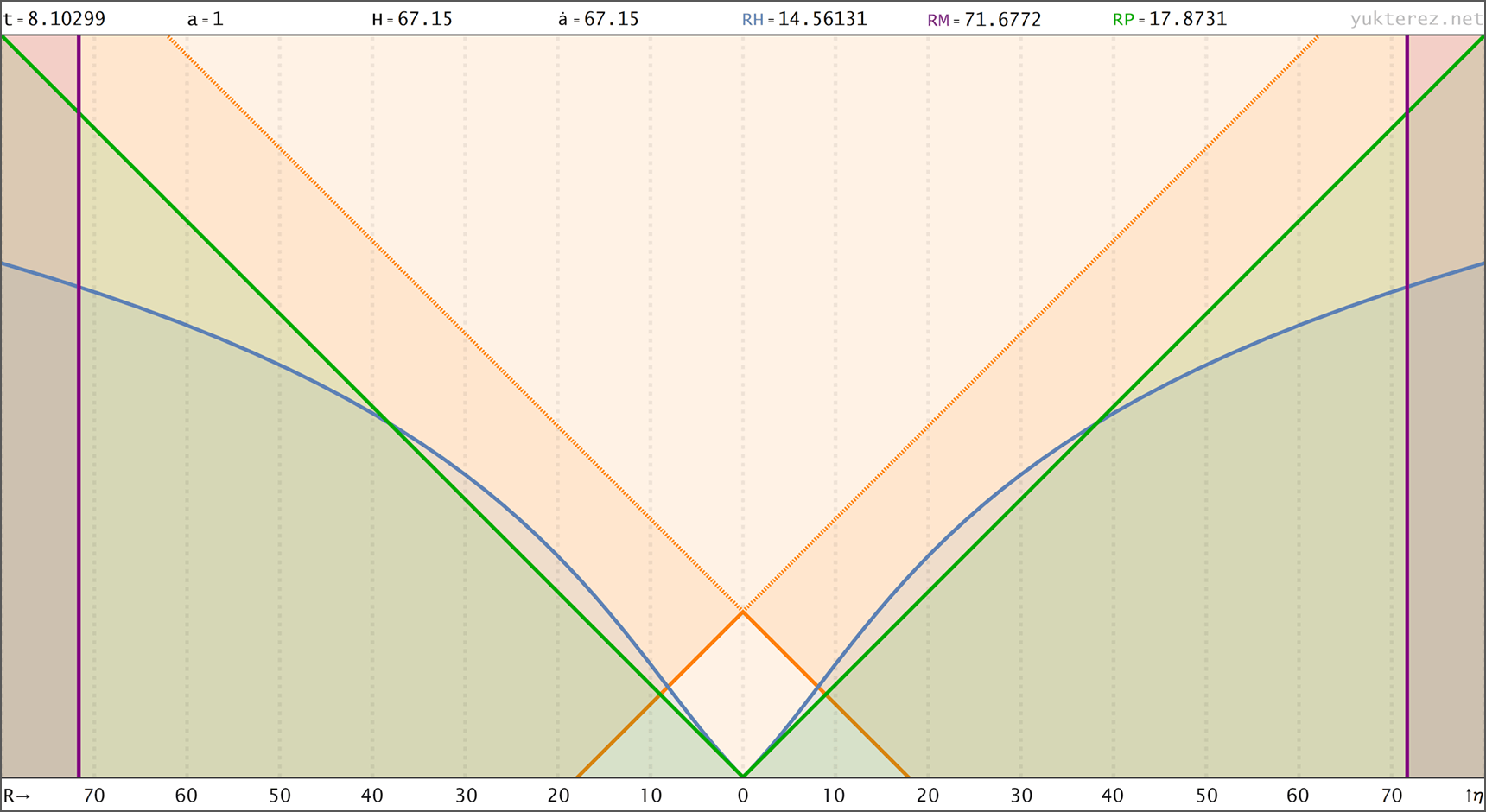
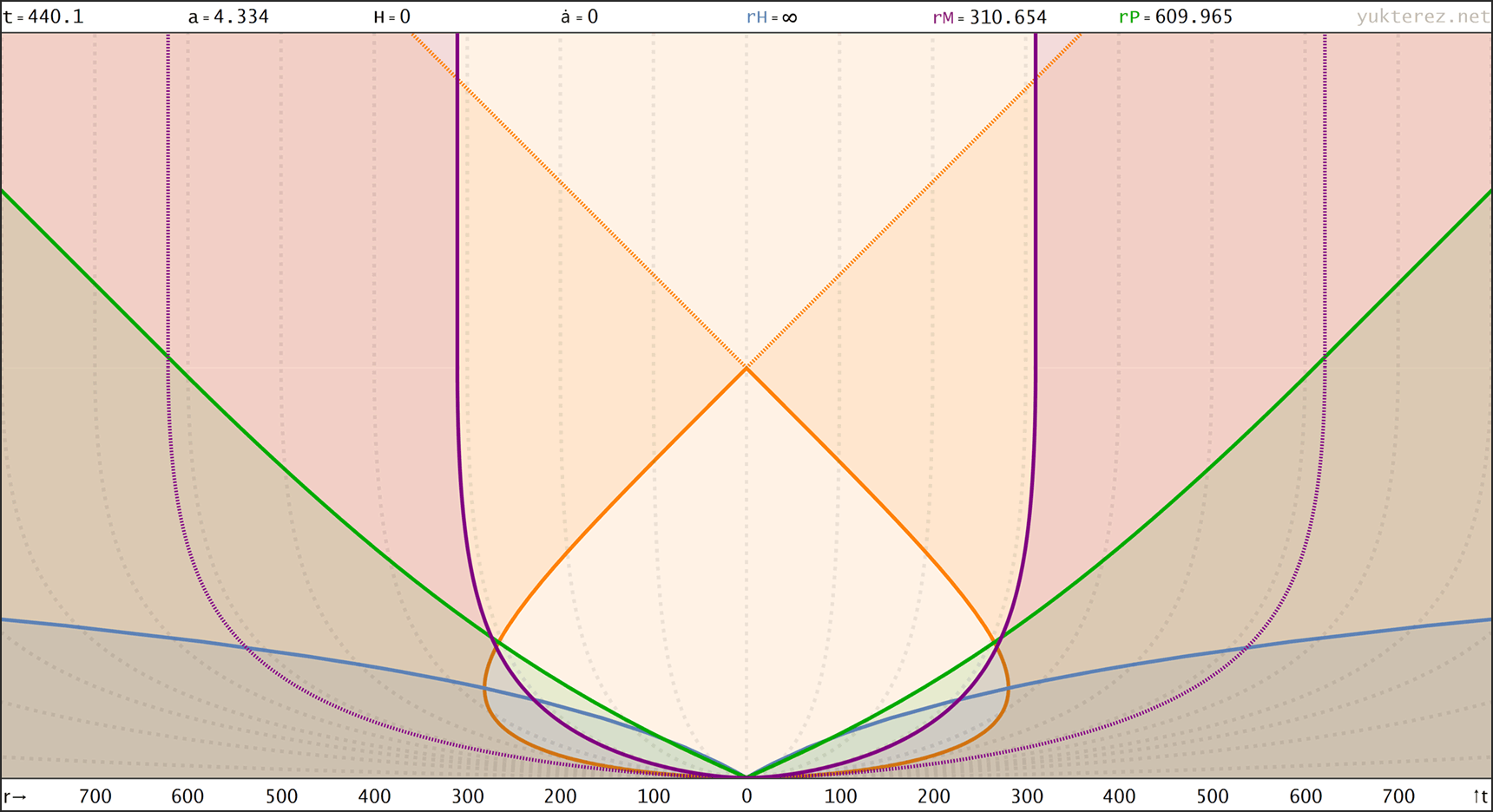
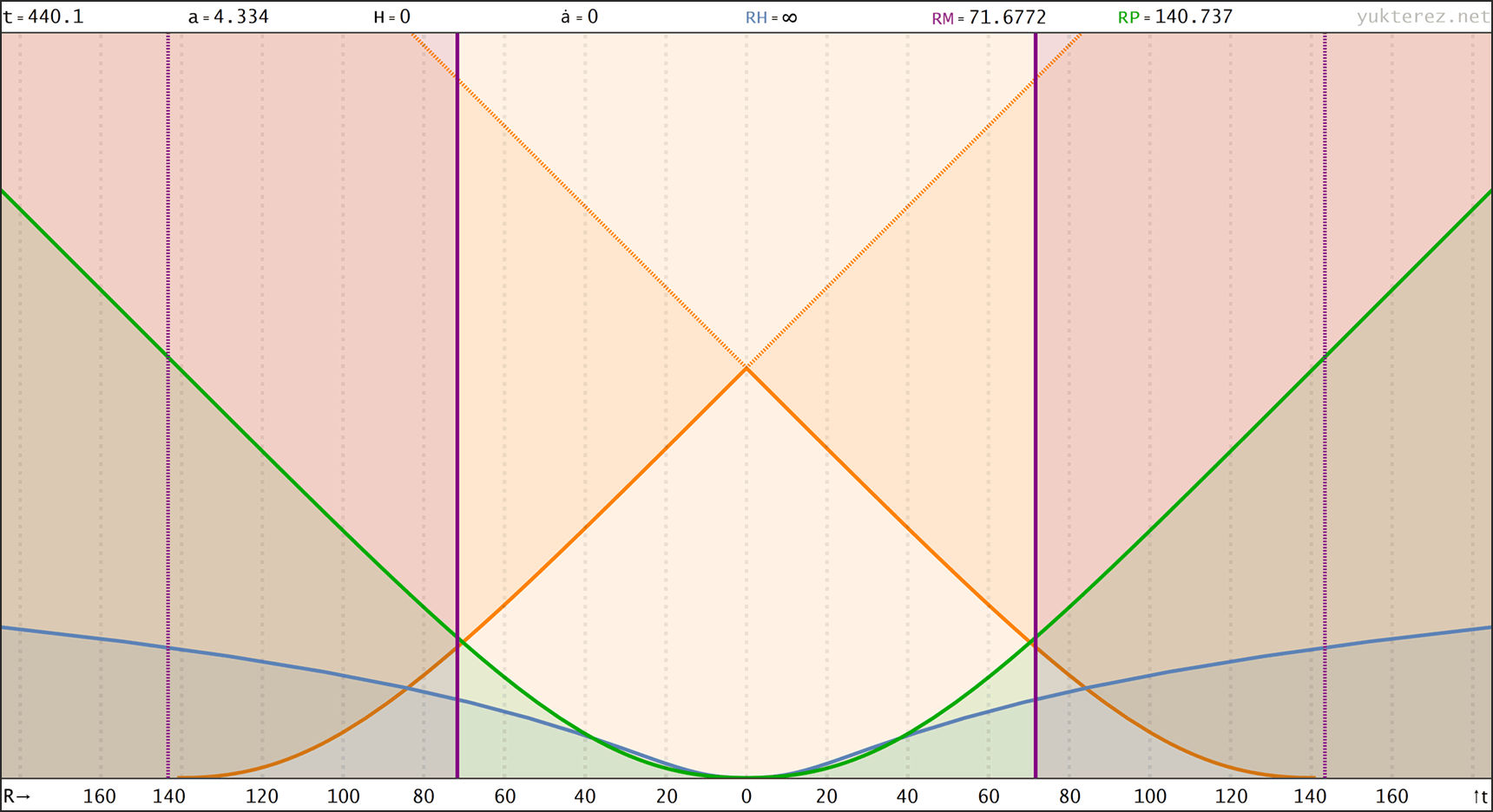
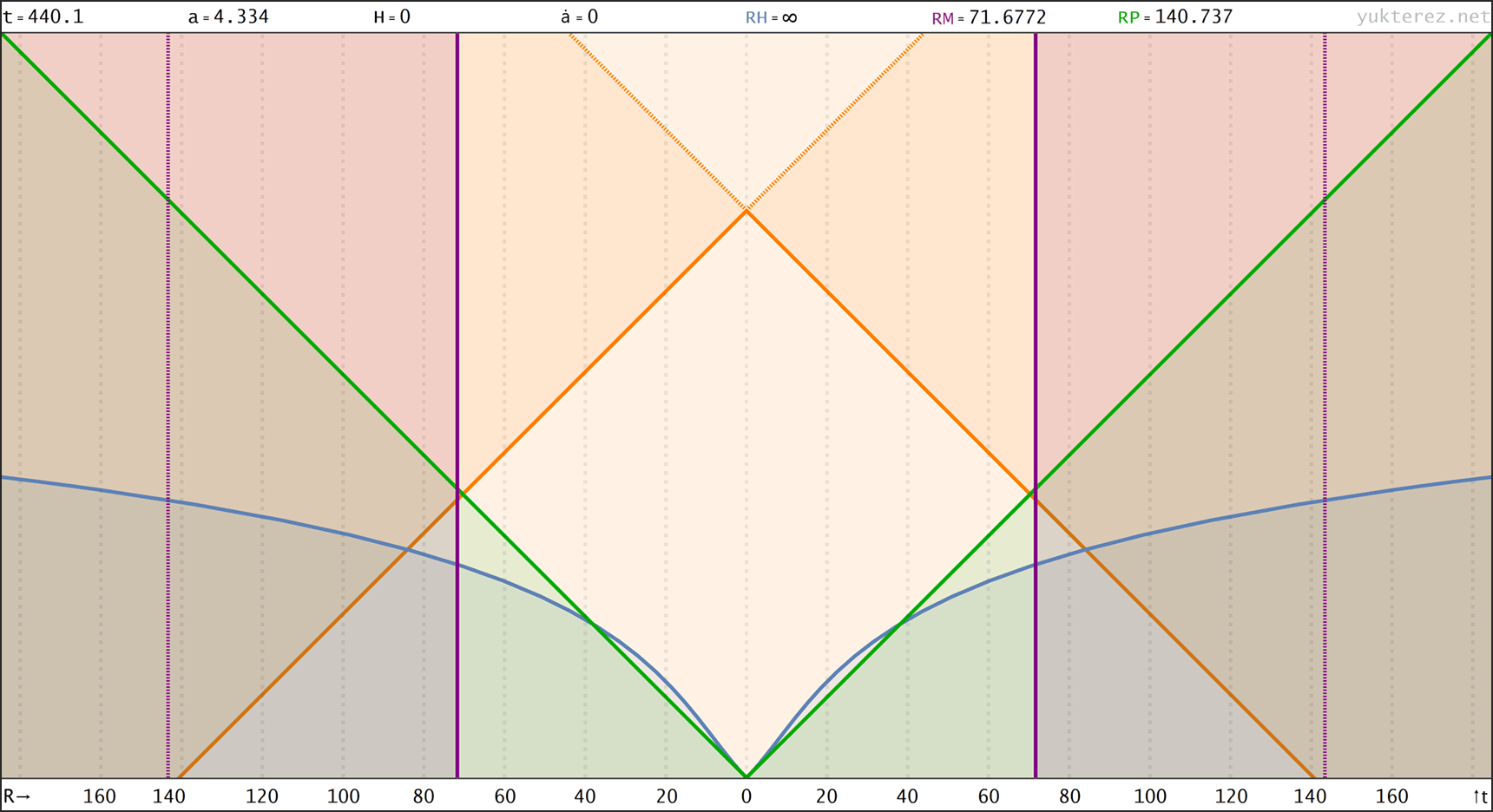
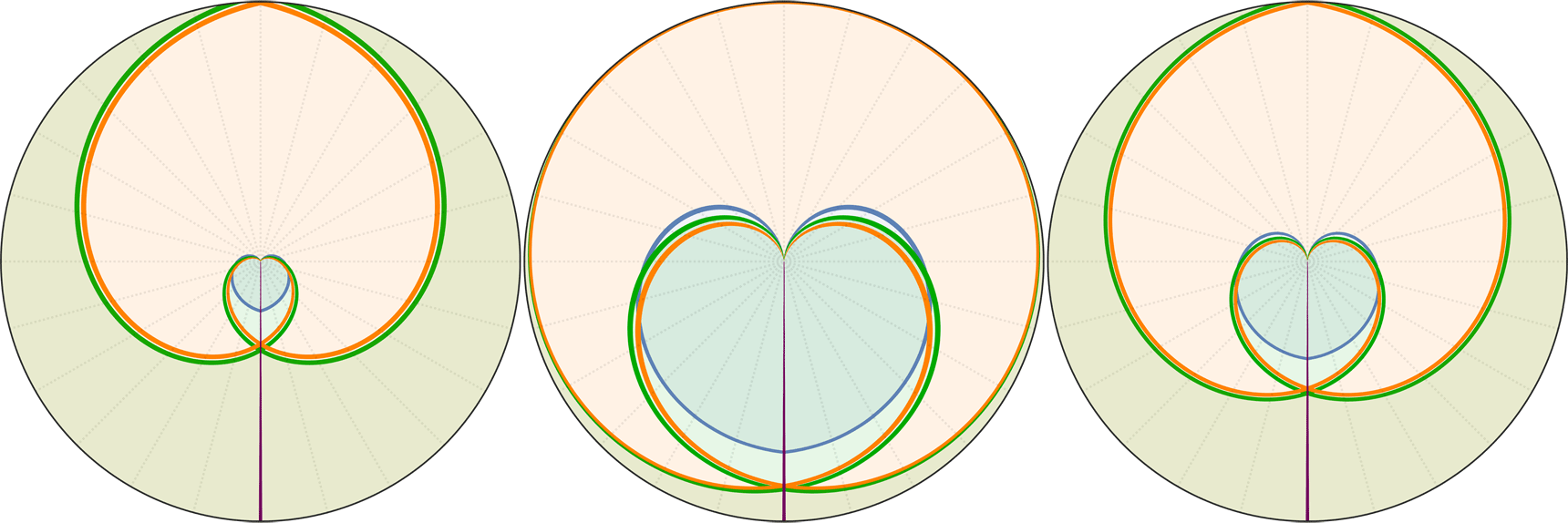
Spacetime diagrams of the universe above in proper distance r(t), comoving distance R(t) & conformal time R(η) coordinates. rH: Hubble radius (blue), rE: Event horizon (none), rP: Particle horizon (green), Orange curve: Past light cone, Dashed orange: Future light cone, Dashed gray: Comoving world lines, R=r/a:


















For the closed FLRW metric in hyperspherical and circumferencial coordinates see here. Spactime diagram code: