Rotierende Ellipse, Funktion
Verfasst: Fr 27. Nov 2015, 00:44
Nachdem die Funktionen die man im Internet zu dem Thema findet zumeist Vorzeichenfehler enthalten oder komplett falsch sind hier die korrekte Gleichung als ContourPlot:
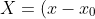 \cos (\omega)- (y-y_0) \sin (\omega))
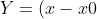 \sin(\omega) + (y - y0) \cos(\omega))
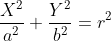
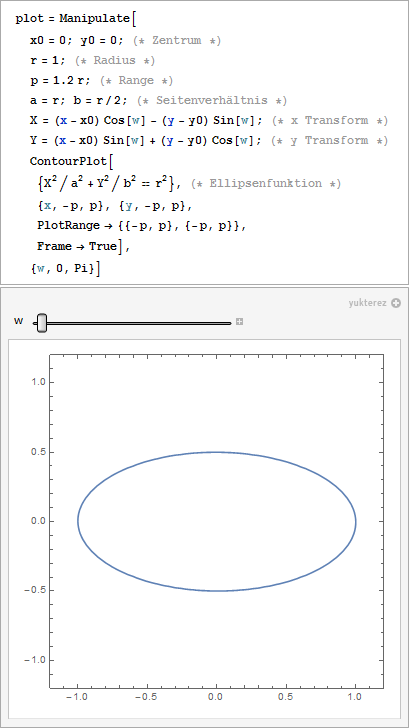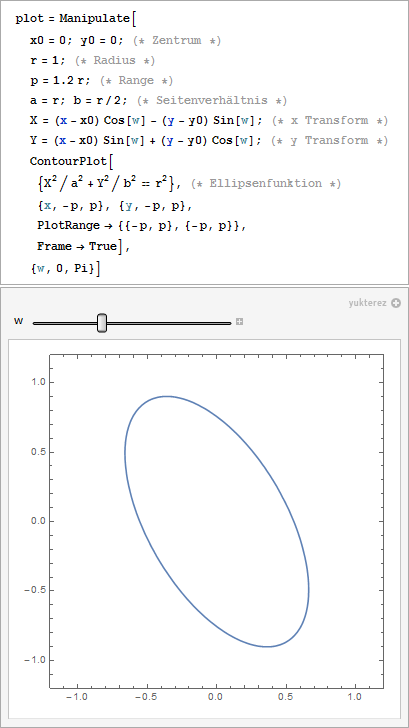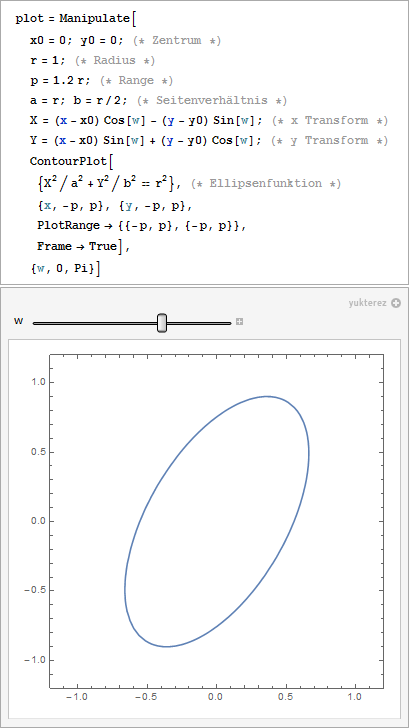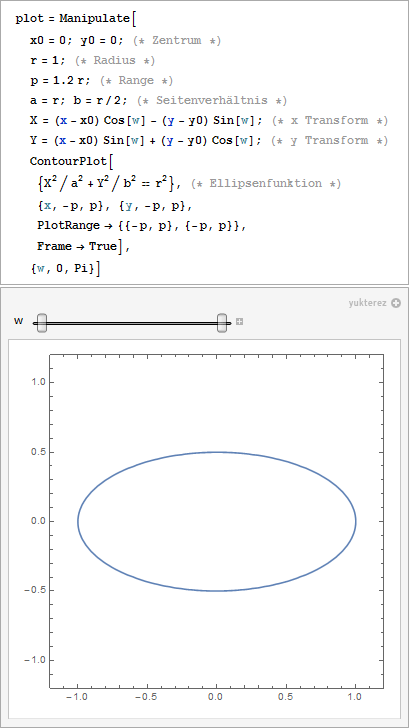
Rotierend,
Koordinaten-Rotation, Coordiante-Rotation, Ellipse, Ellipsoid, Wolfram Mathematica Code
Code: Alles auswählen
plot = Manipulate[
x0 = 0; y0 = 0; (* Zentrum *)
r = 1; (* Radius *)
p = 1.2 r; (* Range *)
a = r; b = r/2; (* Seitenverhältnis *)
X = (x - x0) Cos[w] - (y - y0) Sin[w]; (* x Transform *)
Y = (x - x0) Sin[w] + (y - y0) Cos[w]; (* y Transform *)
ContourPlot[
{X^2/a^2 + Y^2/b^2 == r^2}, (* Standard Ellipsenfunktion *)
{x, -p, p}, {y, -p, p},
PlotRange -> {{-p, p}, {-p, p}},
Frame -> True], {w, 0, Pi}]
Export["ellipse.avi", plot, "FrameRate" -> 250]
Rotierend,
Koordinaten-Rotation, Coordiante-Rotation, Ellipse, Ellipsoid, Wolfram Mathematica Code