Pandemie Rechner
Verfasst: Mo 23. Mär 2020, 02:10

 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  An english translation is available at en.yukterez.net
An english translation is available at en.yukterez.net
SIRD-Modell

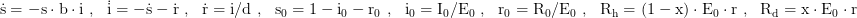
Startbedingungen → E0: insgesamte Einwohner, I0: Infizierte, R0: Genesene und Immunisierte plus Verstorbene, b0 und b1: anfängliche und finale Transmissionsrate, b: zeitabhängige Transmissionsrate.
Parameter → T: Zeitspanne der Integration, tb: Zeitspanne in der sich die Ausbreitungsrate ändert, tu: Zeitspanne bevor die Ausbreitungsrate sich zu ändern beginnt, d: Dauer der Krankheit, h: Hospitalisierungsrate der Infizierten, x: Sterberate der Infizierten, Rh: Genesene und Immunisierte, Rd: Verstorbene.
Die Transmissionsrate kann größer als die effektive Ausbreitungsrate sein; erstere beschreibt im Durchschnitt an wie viele Leute ein Infizierter pro Tag seine Virenladung weitergibt, und letztere wie viele davon auch tatsächlich neu angesteckt werden. Wenn das Produkt aus Transmissionsrate und Krankheitsdauer (der Replikationsfaktor ℛ=b·d) kleiner als 1 ist verringert sich die Anzahl der Infizierten, andernfalls steigt sie.
Code: Alles auswählen
(* pandemic.yukterez.net *)
T = 300; (* Zeitraum *)
E0 = 83000000; (* Einwohner *)
I0 = 66; (* Infizierte *)
R0 = 0; (* Geheilte *)
b0 = 30/100; (* initiale Transmissionsrate *)
b1 = 30/100; (* finale Transmissionsrate *)
tu = 15; (* Zeitspanne der ungehinderten Ausbreitung *)
tb = 5; (* Zeitspanne b0 -> b1 *)
d = 30; (* Krankheitsdauer *)
h = 2/10; (* Hospitalisierungsrate *)
x = 3/100; (* Sterberate *)
f = (b0-b1)/tb; (* Änderung der Transmissionsrate *)
τ = t-tu;
B = If[b0==b1, b0, If[b1<b0, Max[b1, b0-f τ], Min[b1, b0-f τ]]];
b = Interpolation[Table[If[t<tu, b0, B], {t, 0, T, 1}]];
i0 = I0/E0; (* Fraktion der Angesteckten *)
r0 = R0/E0; (* Fraktion der Geheilten *)
s0 = 1-i0-r0; (* Fraktion der Ansteckbaren *)
DGL = {
s'[t] == -s[t] b[t] i[t], (* Änderungsrate der noch Gesunden *)
i'[t] == s[t] b[t] i[t]-i[t]/d, (* Änderungsrate der Infizierten *)
r'[t] == i[t]/d, (* Änderungsrate der Geheilten *)
s[0] == s0,
i[0] == i0,
r[0] == r0};
sol = Quiet[NDSolve[DGL, {s, i, r}, {t, 0, T+tu},
WorkingPrecision -> 48, MaxSteps -> Infinity,
InterpolationOrder -> All]];
max = Quiet[FindMaximum[i[t] /. sol, {t, 1}]]
Plot[{
Evaluate[E0 s[t] /. sol], (* noch gesund, rot *)
Evaluate[E0 i[t] /. sol], (* erkrankt, blau *)
Evaluate[h E0 i[t] /. sol], (* hospitalisiert, schwarz *)
Evaluate[(1-x) E0 r[t] /. sol], (* wieder gesund, grün *)
Evaluate[x E0 r[t] /. sol] (* gestorben, grau *)
}, {t, 0, T},
Frame -> True,
AxesOrigin -> {0, 0},
ImageSize -> 380,
PlotRange -> {All, {0, E0}},
ImagePadding -> {{50, 1}, {20, 10}},
PlotStyle -> {Red, Blue, Black, Green, Gray},
GridLines -> {{t/.max[[2]]}, {E0 max[[1]], E0/2}}]
Framed[Grid[Join[{{
"Tag ",
"Krank (N) ", "Krank (+%) ", "Tot ",
"Spital ", "Gesund ", "Genesen "
}}, {{" ", " ", " ", " ", " "}},
Table[{t,
Round[Evaluate[E0 i[t] /. sol][[1]]],
100 N[Evaluate[(i[t]/i[Max[0, t-1]]-1) /. sol][[1]], 4],
Round[Evaluate[x E0 r[t] /. sol][[1]]],
Round[Evaluate[h E0 i[t] /. sol][[1]]],
Round[Evaluate[E0 s[t] /. sol][[1]]],
Round[Evaluate[(1-x) E0 r[t] /. sol][[1]]]},
{t, 0, T, 1}]],
Alignment -> Left]]
Startparameter: Deutschland, am 29.2.2020, Best Fit: hier wird davon ausgegangen dass die Maßnahmen die am 7.3.2020 begonnen wurden mit einer durchschnittlichen Inkubationsverzögerung von 1 Woche zu wirken beginnen, und die Transmissionsrate im Verlauf von weiteren 11 Tagen in denen die Bevölkerung anfängt die sozialen Kontakte zurückzuschrauben von 0.31 auf 0.15 gesenkt werden kann. Zum Vergleich mit einer konstanten Transmissionsrate klick hier; Plot:

x-Achse: Tage; y-Achse: Personen, %; rot: noch gesund; blau: erkrankt, schwarz: hospitalisiert; grün: genesen; grau: tot. Erklärung: hier entlang Coronavirus, Corona Virus, Covid-19, Sars-Cov-2, Equation, Exponential Growth, Pandemy Mathematics, 2019-nCov Growth Formula


