


Dieser Beitrag ist ein Unterkapitel von nbody.yukterez.net und schwarzschild.yukterez.net

1) Newton (von der Wechselwirkung mit den anderen Planeten stammender Anteil)

Input (der Code wurde 2024 an die neueste Version von Mathematica angepasst):
Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||| Mathematica Syntax || yukterez.net || n Body Newtonian Mass & Charge Simulator ||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
ClearAll["Global`*"]; ClearAll["Local`*"];
Needs["DifferentialEquations`NDSolveProblems`"];
Needs["DifferentialEquations`NDSolveUtilities`"];
Amp = 1; kg = 1; m = 1; sek = 1; km = 1000 m; (* SI Einheiten *)
mt1 = {"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mt2 = {"ImplicitRungeKutta", "DifferenceOrder"-> 20};
mta = mt1;
wp = MachinePrecision;
(* Zeitrahmen *)
T1 = -800 yr;
T2 = -010 yr;
T0 = -810 yr;
(* Konstanten *)
G = 667384/10^16 m^3/kg/sek^2;
ε0 = 8854187817*^-21 Amp^2 sek^4/kg/m^3;
c = 299792458 m/sek;
Au = 149597870700 m;
dy = 24*3600 sek;
yr = 36525*dy/100;
(* Ephemeriden vom 19.02.2019, 0:00:00 TDB *)
(* Sonne *)
m1 = +1.9884350000000000000000000000000*^30 kg;
q1 = +77 Amp sek;
x1x = -1.1471965705032040000000000000000*^-03 Au;
y1y = +7.5150744319204340000000000000000*^-03 Au;
z1z = -4.7302736511930380000000000000000*^-05 Au;
v1x = -8.1079311629029370000000000000000*^-06 Au/dy;
v1y = +1.5208497329286620000000000000000*^-06 Au/dy;
v1z = +2.0955545985674270000000000000000*^-07 Au/dy;
(* Merkur *)
m2 = +3.3010400000000000000000000000000*^23 kg;
q2 = +0 Amp sek;
x2x = +2.4936821875284740000000000000000*^-01 Au;
y2y = +2.0608486672780060000000000000000*^-01 Au;
z2z = -6.8031627767377100000000000000000*^-03 Au;
v2x = -2.3018288522526540000000000000000*^-02 Au/dy;
v2y = +2.3260031991339930000000000000000*^-02 Au/dy;
v2z = +4.0116405390833950000000000000000*^-03 Au/dy;
(* Venus *)
m3 = +4.8673200000000000000000000000000*^24 kg;
q3 = +0 Amp sek;
x3x = -5.6045726002672760000000000000000*^-01 Au;
y3y = -4.5005542704084160000000000000000*^-01 Au;
z3z = +2.5950732468947320000000000000000*^-02 Au;
v3x = +1.2656894620948180000000000000000*^-02 Au/dy;
v3y = -1.5748296388765200000000000000000*^-02 Au/dy;
v3z = -9.4676526908447310000000000000000*^-04 Au/dy;
(* Erde + Mond *)
m4 = +5.9721986000000000000000000000000*^24 kg+
7.3459000000000000000000000000000*^22 kg;
q4 = +0 Amp sek;
x4x = -8.5520721638344890000000000000000*^-01 Au;
y4y = +5.0497150218223640000000000000000*^-01 Au;
z4z = -6.8498775458511310000000000000000*^-05 Au;
v4x = -8.9429125681162910000000000000000*^-03 Au/dy;
v4y = -1.4923656785031820000000000000000*^-02 Au/dy;
v4z = +2.7411786226946430000000000000000*^-07 Au/dy;
(* Mars *)
m5 = +6.4169300000000000000000000000000*^23 kg;
q5 = +0 Amp sek;
x5x = +5.5807246057361930000000000000000*^-01 Au;
y5y = +1.4162615722015340000000000000000*^+00 Au;
z5z = +1.5749250827409650000000000000000*^-02 Au;
v5x = -1.2485440194878080000000000000000*^-02 Au/dy;
v5y = +6.3550834170083260000000000000000*^-03 Au/dy;
v5z = +4.3949929473866280000000000000000*^-04 Au/dy;
(* Jupiter *)
m6 = +1.8981300000000000000000000000000*^27 kg;
q6 = +0 Amp sek;
x6x = -1.7958218609266940000000000000000*^+00 Au;
y6y = -5.0164691671747720000000000000000*^+00 Au;
z6z = +6.0975871803082480000000000000000*^-02 Au;
v6x = +7.0145258242563180000000000000000*^-03 Au/dy;
v6y = -2.1830109907967640000000000000000*^-03 Au/dy;
v6z = -1.4780907747433380000000000000000*^-04 Au/dy;
(* Saturn *)
m7 = +5.6831900000000000000000000000000*^26 kg;
q7 = +0 Amp sek;
x7x = +2.2111653513805970000000000000000*^+00 Au;
y7y = -9.8038462167238740000000000000000*^+00 Au;
z7z = +8.2444750370636570000000000000000*^-02 Au;
v7x = +5.1339650655565250000000000000000*^-03 Au/dy;
v7y = +1.2103335904716640000000000000000*^-03 Au/dy;
v7z = -2.2558556212364290000000000000000*^-04 Au/dy;
(* Uranus *)
m8 = +8.6810300000000000000000000000000*^25 kg;
q8 = +0 Amp sek;
x8x = +1.6913675729610520000000000000000*^+01 Au;
y8y = +1.0406159640425210000000000000000*^+01 Au;
z8z = -1.8047020521229500000000000000000*^-01 Au;
v8x = -2.0899333727330800000000000000000*^-03 Au/dy;
v8y = +3.1665490642136050000000000000000*^-03 Au/dy;
v8z = +3.8840935617397330000000000000000*^-05 Au/dy;
(* Neptun *)
m9 = +1.0241300000000000000000000000000*^26 kg;
q9 = +0 Amp sek;
x9x = +2.9018674808632950000000000000000*^+01 Au;
y9y = -7.3312603965211460000000000000000*^+00 Au;
z9z = -5.1779147377347610000000000000000*^-01 Au;
v9x = +7.4761314057479110000000000000000*^-04 Au/dy;
v9y = +3.0621016427902180000000000000000*^-03 Au/dy;
v9z = -8.0008400968531150000000000000000*^-05 Au/dy;
(* Pluto + Charon *)
m0 = +1.3030000000000000000000000000000*^22 kg+
1.5860000000000000000000000000000*^21 kg;
q0 = +0 Amp sek;
x0x = +1.2028946125005490000000000000000*^+01 Au;
y0y = -3.1518782215680630000000000000000*^+01 Au;
z0z = -1.0678122487212660000000000000000*^-01 Au;
v0x = +3.0044279222551820000000000000000*^-03 Au/dy;
v0y = +4.5018983443458730000000000000000*^-04 Au/dy;
v0z = -9.2990301656806090000000000000000*^-04 Au/dy;
(* Differentialgleichung *)
nds=NDSolve[{
x1'[t] == vx1[t], y1'[t] == vy1[t], z1'[t] == vz1[t],
x2'[t] == vx2[t], y2'[t] == vy2[t], z2'[t] == vz2[t],
x3'[t] == vx3[t], y3'[t] == vy3[t], z3'[t] == vz3[t],
x4'[t] == vx4[t], y4'[t] == vy4[t], z4'[t] == vz4[t],
x5'[t] == vx5[t], y5'[t] == vy5[t], z5'[t] == vz5[t],
x6'[t] == vx6[t], y6'[t] == vy6[t], z6'[t] == vz6[t],
x7'[t] == vx7[t], y7'[t] == vy7[t], z7'[t] == vz7[t],
x8'[t] == vx8[t], y8'[t] == vy8[t], z8'[t] == vz8[t],
x9'[t] == vx9[t], y9'[t] == vy9[t], z9'[t] == vz9[t],
x0'[t] == vx0[t], y0'[t] == vy0[t], z0'[t] == vz0[t],
vx1'[t] ==
(G m2 (x2[t]-x1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(G m3 (x3[t]-x1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(G m4 (x4[t]-x1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(G m5 (x5[t]-x1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(G m6 (x6[t]-x1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(G m7 (x7[t]-x1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(G m8 (x8[t]-x1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(G m9 (x9[t]-x1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(G m0 (x0[t]-x1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]+
If[q1 == 0, 0,
(-q1*q2/(4π ε0 )/m1 (x2[t]-x1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(-q1*q3/(4π ε0 )/m1 (x3[t]-x1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(-q1*q4/(4π ε0 )/m1 (x4[t]-x1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(-q1*q5/(4π ε0 )/m1 (x5[t]-x1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(-q1*q6/(4π ε0 )/m1 (x6[t]-x1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(-q1*q7/(4π ε0 )/m1 (x7[t]-x1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(-q1*q8/(4π ε0 )/m1 (x8[t]-x1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(-q1*q9/(4π ε0 )/m1 (x9[t]-x1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(-q1*q0/(4π ε0 )/m1 (x0[t]-x1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]],
vy1'[t] ==
(G m2 (y2[t]-y1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(G m3 (y3[t]-y1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(G m4 (y4[t]-y1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(G m5 (y5[t]-y1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(G m6 (y6[t]-y1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(G m7 (y7[t]-y1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(G m8 (y8[t]-y1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(G m9 (y9[t]-y1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(G m0 (y0[t]-y1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]+
If[q1 == 0, 0,
(-q1*q2/(4π ε0 )/m1 (y2[t]-y1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(-q1*q3/(4π ε0 )/m1 (y3[t]-y1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(-q1*q4/(4π ε0 )/m1 (y4[t]-y1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(-q1*q5/(4π ε0 )/m1 (y5[t]-y1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(-q1*q6/(4π ε0 )/m1 (y6[t]-y1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(-q1*q7/(4π ε0 )/m1 (y7[t]-y1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(-q1*q8/(4π ε0 )/m1 (y8[t]-y1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(-q1*q9/(4π ε0 )/m1 (y9[t]-y1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(-q1*q0/(4π ε0 )/m1 (y0[t]-y1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]],
vz1'[t] ==
(G m2 (z2[t]-z1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(G m3 (z3[t]-z1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(G m4 (z4[t]-z1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(G m5 (z5[t]-z1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(G m6 (z6[t]-z1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(G m7 (z7[t]-z1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(G m8 (z8[t]-z1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(G m9 (z9[t]-z1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(G m0 (z0[t]-z1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]+
If[q1 == 0, 0,
(-q1*q2/(4π ε0 )/m1 (z2[t]-z1[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(-q1*q3/(4π ε0 )/m1 (z3[t]-z1[t]))/Sqrt[((x3[t]-x1[t])^2+(y3[t]-y1[t])^2+(z3[t]-z1[t])^2)^3]+
(-q1*q4/(4π ε0 )/m1 (z4[t]-z1[t]))/Sqrt[((x4[t]-x1[t])^2+(y4[t]-y1[t])^2+(z4[t]-z1[t])^2)^3]+
(-q1*q5/(4π ε0 )/m1 (z5[t]-z1[t]))/Sqrt[((x5[t]-x1[t])^2+(y5[t]-y1[t])^2+(z5[t]-z1[t])^2)^3]+
(-q1*q6/(4π ε0 )/m1 (z6[t]-z1[t]))/Sqrt[((x6[t]-x1[t])^2+(y6[t]-y1[t])^2+(z6[t]-z1[t])^2)^3]+
(-q1*q7/(4π ε0 )/m1 (z7[t]-z1[t]))/Sqrt[((x7[t]-x1[t])^2+(y7[t]-y1[t])^2+(z7[t]-z1[t])^2)^3]+
(-q1*q8/(4π ε0 )/m1 (z8[t]-z1[t]))/Sqrt[((x8[t]-x1[t])^2+(y8[t]-y1[t])^2+(z8[t]-z1[t])^2)^3]+
(-q1*q9/(4π ε0 )/m1 (z9[t]-z1[t]))/Sqrt[((x9[t]-x1[t])^2+(y9[t]-y1[t])^2+(z9[t]-z1[t])^2)^3]+
(-q1*q0/(4π ε0 )/m1 (z0[t]-z1[t]))/Sqrt[((x0[t]-x1[t])^2+(y0[t]-y1[t])^2+(z0[t]-z1[t])^2)^3]],
vx2'[t] ==
(G m1 (x1[t]-x2[t]))/Sqrt[((x1[t]-x2[t])^2+(y1[t]-y2[t])^2+(z1[t]-z2[t])^2)^3]+
(G m3 (x3[t]-x2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(G m4 (x4[t]-x2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(G m5 (x5[t]-x2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(G m6 (x6[t]-x2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(G m7 (x7[t]-x2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(G m8 (x8[t]-x2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(G m9 (x9[t]-x2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(G m0 (x0[t]-x2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]+
If[q2 == 0, 0,
(-q2*q1/(4π ε0 )/m2 (x1[t]-x2[t]))/Sqrt[((x1[t]-x2[t])^2+(y1[t]-y2[t])^2+(z1[t]-z2[t])^2)^3]+
(-q2*q3/(4π ε0 )/m2 (x3[t]-x2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(-q2*q4/(4π ε0 )/m2 (x4[t]-x2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(-q2*q5/(4π ε0 )/m2 (x5[t]-x2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(-q2*q6/(4π ε0 )/m2 (x6[t]-x2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(-q2*q7/(4π ε0 )/m2 (x7[t]-x2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(-q2*q8/(4π ε0 )/m2 (x8[t]-x2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(-q2*q9/(4π ε0 )/m2 (x9[t]-x2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(-q2*q0/(4π ε0 )/m2 (x0[t]-x2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]],
vy2'[t] ==
(G m1 (y1[t]-y2[t]))/Sqrt[((x1[t]-x2[t])^2+(y1[t]-y2[t])^2+(z1[t]-z2[t])^2)^3]+
(G m3 (y3[t]-y2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(G m4 (y4[t]-y2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(G m5 (y5[t]-y2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(G m6 (y6[t]-y2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(G m7 (y7[t]-y2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(G m8 (y8[t]-y2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(G m9 (y9[t]-y2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(G m0 (y0[t]-y2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]+
If[q2 == 0, 0,
(-q2*q1/(4π ε0 )/m2 (y1[t]-y2[t]))/Sqrt[((x1[t]-x2[t])^2+(y1[t]-y2[t])^2+(z1[t]-z2[t])^2)^3]+
(-q2*q3/(4π ε0 )/m2 (y3[t]-y2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(-q2*q4/(4π ε0 )/m2 (y4[t]-y2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(-q2*q5/(4π ε0 )/m2 (y5[t]-y2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(-q2*q6/(4π ε0 )/m2 (y6[t]-y2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(-q2*q7/(4π ε0 )/m2 (y7[t]-y2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(-q2*q8/(4π ε0 )/m2 (y8[t]-y2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(-q2*q9/(4π ε0 )/m2 (y9[t]-y2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(-q2*q0/(4π ε0 )/m2 (y0[t]-y2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]],
vz2'[t] ==
(G m1 (z1[t]-z2[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(G m3 (z3[t]-z2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(G m4 (z4[t]-z2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(G m5 (z5[t]-z2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(G m6 (z6[t]-z2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(G m7 (z7[t]-z2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(G m8 (z8[t]-z2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(G m9 (z9[t]-z2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(G m0 (z0[t]-z2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]+
If[q2 == 0, 0,
(-q2*q1/(4π ε0 )/m2 (z1[t]-z2[t]))/Sqrt[((x2[t]-x1[t])^2+(y2[t]-y1[t])^2+(z2[t]-z1[t])^2)^3]+
(-q2*q3/(4π ε0 )/m2 (z3[t]-z2[t]))/Sqrt[((x3[t]-x2[t])^2+(y3[t]-y2[t])^2+(z3[t]-z2[t])^2)^3]+
(-q2*q4/(4π ε0 )/m2 (z4[t]-z2[t]))/Sqrt[((x4[t]-x2[t])^2+(y4[t]-y2[t])^2+(z4[t]-z2[t])^2)^3]+
(-q2*q5/(4π ε0 )/m2 (z5[t]-z2[t]))/Sqrt[((x5[t]-x2[t])^2+(y5[t]-y2[t])^2+(z5[t]-z2[t])^2)^3]+
(-q2*q6/(4π ε0 )/m2 (z6[t]-z2[t]))/Sqrt[((x6[t]-x2[t])^2+(y6[t]-y2[t])^2+(z6[t]-z2[t])^2)^3]+
(-q2*q7/(4π ε0 )/m2 (z7[t]-z2[t]))/Sqrt[((x7[t]-x2[t])^2+(y7[t]-y2[t])^2+(z7[t]-z2[t])^2)^3]+
(-q2*q8/(4π ε0 )/m2 (z8[t]-z2[t]))/Sqrt[((x8[t]-x2[t])^2+(y8[t]-y2[t])^2+(z8[t]-z2[t])^2)^3]+
(-q2*q9/(4π ε0 )/m2 (z9[t]-z2[t]))/Sqrt[((x9[t]-x2[t])^2+(y9[t]-y2[t])^2+(z9[t]-z2[t])^2)^3]+
(-q2*q0/(4π ε0 )/m2 (z0[t]-z2[t]))/Sqrt[((x0[t]-x2[t])^2+(y0[t]-y2[t])^2+(z0[t]-z2[t])^2)^3]],
vx3'[t] ==
(G m1 (x1[t]-x3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(G m2 (x2[t]-x3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(G m4 (x4[t]-x3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(G m5 (x5[t]-x3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(G m6 (x6[t]-x3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(G m7 (x7[t]-x3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(G m8 (x8[t]-x3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(G m9 (x9[t]-x3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(G m0 (x0[t]-x3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]+
If[q3 == 0, 0,
(-q3*q1/(4π ε0 )/m3 (x1[t]-x3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(-q3*q2/(4π ε0 )/m3 (x2[t]-x3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(-q3*q4/(4π ε0 )/m3 (x4[t]-x3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(-q3*q5/(4π ε0 )/m3 (x5[t]-x3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(-q3*q6/(4π ε0 )/m3 (x6[t]-x3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(-q3*q7/(4π ε0 )/m3 (x7[t]-x3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(-q3*q8/(4π ε0 )/m3 (x8[t]-x3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(-q3*q9/(4π ε0 )/m3 (x9[t]-x3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(-q3*q0/(4π ε0 )/m3 (x0[t]-x3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]],
vy3'[t] ==
(G m1 (y1[t]-y3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(G m2 (y2[t]-y3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(G m4 (y4[t]-y3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(G m5 (y5[t]-y3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(G m6 (y6[t]-y3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(G m7 (y7[t]-y3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(G m8 (y8[t]-y3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(G m9 (y9[t]-y3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(G m0 (y0[t]-y3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]+
If[q3 == 0, 0,
(-q3*q1/(4π ε0 )/m3 (y1[t]-y3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(-q3*q2/(4π ε0 )/m3 (y2[t]-y3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(-q3*q4/(4π ε0 )/m3 (y4[t]-y3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(-q3*q5/(4π ε0 )/m3 (y5[t]-y3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(-q3*q6/(4π ε0 )/m3 (y6[t]-y3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(-q3*q7/(4π ε0 )/m3 (y7[t]-y3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(-q3*q8/(4π ε0 )/m3 (y8[t]-y3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(-q3*q9/(4π ε0 )/m3 (y9[t]-y3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(-q3*q0/(4π ε0 )/m3 (y0[t]-y3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]],
vz3'[t] ==
(G m1 (z1[t]-z3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(G m2 (z2[t]-z3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(G m4 (z4[t]-z3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(G m5 (z5[t]-z3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(G m6 (z6[t]-z3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(G m7 (z7[t]-z3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(G m8 (z8[t]-z3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(G m9 (z9[t]-z3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(G m0 (z0[t]-z3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]+
If[q3 == 0, 0,
(-q3*q1/(4π ε0 )/m3 (z1[t]-z3[t]))/Sqrt[((x1[t]-x3[t])^2+(y1[t]-y3[t])^2+(z1[t]-z3[t])^2)^3]+
(-q3*q2/(4π ε0 )/m3 (z2[t]-z3[t]))/Sqrt[((x2[t]-x3[t])^2+(y2[t]-y3[t])^2+(z2[t]-z3[t])^2)^3]+
(-q3*q4/(4π ε0 )/m3 (z4[t]-z3[t]))/Sqrt[((x4[t]-x3[t])^2+(y4[t]-y3[t])^2+(z4[t]-z3[t])^2)^3]+
(-q3*q5/(4π ε0 )/m3 (z5[t]-z3[t]))/Sqrt[((x5[t]-x3[t])^2+(y5[t]-y3[t])^2+(z5[t]-z3[t])^2)^3]+
(-q3*q6/(4π ε0 )/m3 (z6[t]-z3[t]))/Sqrt[((x6[t]-x3[t])^2+(y6[t]-y3[t])^2+(z6[t]-z3[t])^2)^3]+
(-q3*q7/(4π ε0 )/m3 (z7[t]-z3[t]))/Sqrt[((x7[t]-x3[t])^2+(y7[t]-y3[t])^2+(z7[t]-z3[t])^2)^3]+
(-q3*q8/(4π ε0 )/m3 (z8[t]-z3[t]))/Sqrt[((x8[t]-x3[t])^2+(y8[t]-y3[t])^2+(z8[t]-z3[t])^2)^3]+
(-q3*q9/(4π ε0 )/m3 (z9[t]-z3[t]))/Sqrt[((x9[t]-x3[t])^2+(y9[t]-y3[t])^2+(z9[t]-z3[t])^2)^3]+
(-q3*q0/(4π ε0 )/m3 (z0[t]-z3[t]))/Sqrt[((x0[t]-x3[t])^2+(y0[t]-y3[t])^2+(z0[t]-z3[t])^2)^3]],
vx4'[t] ==
(G m1 (x1[t]-x4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(G m2 (x2[t]-x4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(G m3 (x3[t]-x4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(G m5 (x5[t]-x4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(G m6 (x6[t]-x4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(G m7 (x7[t]-x4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(G m8 (x8[t]-x4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(G m9 (x9[t]-x4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(G m0 (x0[t]-x4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]+
If[q4 == 0, 0,
(-q4*q1/(4π ε0 )/m4 (x1[t]-x4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(-q4*q2/(4π ε0 )/m4 (x2[t]-x4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(-q4*q3/(4π ε0 )/m4 (x3[t]-x4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(-q4*q5/(4π ε0 )/m4 (x5[t]-x4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(-q4*q6/(4π ε0 )/m4 (x6[t]-x4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(-q4*q7/(4π ε0 )/m4 (x7[t]-x4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(-q4*q8/(4π ε0 )/m4 (x8[t]-x4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(-q4*q9/(4π ε0 )/m4 (x9[t]-x4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(-q4*q0/(4π ε0 )/m4 (x0[t]-x4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]],
vy4'[t] ==
(G m1 (y1[t]-y4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(G m2 (y2[t]-y4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(G m3 (y3[t]-y4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(G m5 (y5[t]-y4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(G m6 (y6[t]-y4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(G m7 (y7[t]-y4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(G m8 (y8[t]-y4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(G m9 (y9[t]-y4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(G m0 (y0[t]-y4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]+
If[q4 == 0, 0,
(-q4*q1/(4π ε0 )/m4 (y1[t]-y4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(-q4*q2/(4π ε0 )/m4 (y2[t]-y4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(-q4*q3/(4π ε0 )/m4 (y3[t]-y4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(-q4*q5/(4π ε0 )/m4 (y5[t]-y4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(-q4*q6/(4π ε0 )/m4 (y6[t]-y4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(-q4*q7/(4π ε0 )/m4 (y7[t]-y4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(-q4*q8/(4π ε0 )/m4 (y8[t]-y4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(-q4*q9/(4π ε0 )/m4 (y9[t]-y4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(-q4*q0/(4π ε0 )/m4 (y0[t]-y4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]],
vz4'[t] ==
(G m1 (z1[t]-z4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(G m2 (z2[t]-z4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(G m3 (z3[t]-z4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(G m5 (z5[t]-z4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(G m6 (z6[t]-z4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(G m7 (z7[t]-z4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(G m8 (z8[t]-z4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(G m9 (z9[t]-z4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(G m0 (z0[t]-z4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]+
If[q4 == 0, 0,
(-q4*q1/(4π ε0 )/m4 (z1[t]-z4[t]))/Sqrt[((x1[t]-x4[t])^2+(y1[t]-y4[t])^2+(z1[t]-z4[t])^2)^3]+
(-q4*q2/(4π ε0 )/m4 (z2[t]-z4[t]))/Sqrt[((x2[t]-x4[t])^2+(y2[t]-y4[t])^2+(z2[t]-z4[t])^2)^3]+
(-q4*q3/(4π ε0 )/m4 (z3[t]-z4[t]))/Sqrt[((x3[t]-x4[t])^2+(y3[t]-y4[t])^2+(z3[t]-z4[t])^2)^3]+
(-q4*q5/(4π ε0 )/m4 (z5[t]-z4[t]))/Sqrt[((x5[t]-x4[t])^2+(y5[t]-y4[t])^2+(z5[t]-z4[t])^2)^3]+
(-q4*q6/(4π ε0 )/m4 (z6[t]-z4[t]))/Sqrt[((x6[t]-x4[t])^2+(y6[t]-y4[t])^2+(z6[t]-z4[t])^2)^3]+
(-q4*q7/(4π ε0 )/m4 (z7[t]-z4[t]))/Sqrt[((x7[t]-x4[t])^2+(y7[t]-y4[t])^2+(z7[t]-z4[t])^2)^3]+
(-q4*q8/(4π ε0 )/m4 (z8[t]-z4[t]))/Sqrt[((x8[t]-x4[t])^2+(y8[t]-y4[t])^2+(z8[t]-z4[t])^2)^3]+
(-q4*q9/(4π ε0 )/m4 (z9[t]-z4[t]))/Sqrt[((x9[t]-x4[t])^2+(y9[t]-y4[t])^2+(z9[t]-z4[t])^2)^3]+
(-q4*q0/(4π ε0 )/m4 (z0[t]-z4[t]))/Sqrt[((x0[t]-x4[t])^2+(y0[t]-y4[t])^2+(z0[t]-z4[t])^2)^3]],
vx5'[t] ==
(G m1 (x1[t]-x5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(G m2 (x2[t]-x5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(G m3 (x3[t]-x5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(G m4 (x4[t]-x5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(G m6 (x6[t]-x5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(G m7 (x7[t]-x5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(G m8 (x8[t]-x5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(G m9 (x9[t]-x5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(G m0 (x0[t]-x5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]+
If[q5 == 0, 0,
(-q5*q1/(4π ε0 )/m5 (x1[t]-x5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(-q5*q2/(4π ε0 )/m5 (x2[t]-x5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(-q5*q3/(4π ε0 )/m5 (x3[t]-x5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(-q5*q4/(4π ε0 )/m5 (x4[t]-x5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(-q5*q6/(4π ε0 )/m5 (x6[t]-x5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(-q5*q7/(4π ε0 )/m5 (x7[t]-x5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(-q5*q8/(4π ε0 )/m5 (x8[t]-x5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(-q5*q9/(4π ε0 )/m5 (x9[t]-x5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(-q5*q0/(4π ε0 )/m5 (x0[t]-x5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]],
vy5'[t] ==
(G m1 (y1[t]-y5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(G m2 (y2[t]-y5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(G m3 (y3[t]-y5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(G m4 (y4[t]-y5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(G m6 (y6[t]-y5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(G m7 (y7[t]-y5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(G m8 (y8[t]-y5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(G m9 (y9[t]-y5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(G m0 (y0[t]-y5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]+
If[q5 == 0, 0,
(-q5*q1/(4π ε0 )/m5 (y1[t]-y5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(-q5*q2/(4π ε0 )/m5 (y2[t]-y5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(-q5*q3/(4π ε0 )/m5 (y3[t]-y5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(-q5*q4/(4π ε0 )/m5 (y4[t]-y5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(-q5*q6/(4π ε0 )/m5 (y6[t]-y5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(-q5*q7/(4π ε0 )/m5 (y7[t]-y5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(-q5*q8/(4π ε0 )/m5 (y8[t]-y5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(-q5*q9/(4π ε0 )/m5 (y9[t]-y5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(-q5*q0/(4π ε0 )/m5 (y0[t]-y5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]],
vz5'[t] ==
(G m1 (z1[t]-z5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(G m2 (z2[t]-z5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(G m3 (z3[t]-z5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(G m4 (z4[t]-z5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(G m6 (z6[t]-z5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(G m7 (z7[t]-z5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(G m8 (z8[t]-z5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(G m9 (z9[t]-z5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(G m0 (z0[t]-z5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]+
If[q5 == 0, 0,
(-q5*q1/(4π ε0 )/m5 (z1[t]-z5[t]))/Sqrt[((x1[t]-x5[t])^2+(y1[t]-y5[t])^2+(z1[t]-z5[t])^2)^3]+
(-q5*q2/(4π ε0 )/m5 (z2[t]-z5[t]))/Sqrt[((x2[t]-x5[t])^2+(y2[t]-y5[t])^2+(z2[t]-z5[t])^2)^3]+
(-q5*q3/(4π ε0 )/m5 (z3[t]-z5[t]))/Sqrt[((x3[t]-x5[t])^2+(y3[t]-y5[t])^2+(z3[t]-z5[t])^2)^3]+
(-q5*q4/(4π ε0 )/m5 (z4[t]-z5[t]))/Sqrt[((x4[t]-x5[t])^2+(y4[t]-y5[t])^2+(z4[t]-z5[t])^2)^3]+
(-q5*q6/(4π ε0 )/m5 (z6[t]-z5[t]))/Sqrt[((x6[t]-x5[t])^2+(y6[t]-y5[t])^2+(z6[t]-z5[t])^2)^3]+
(-q5*q7/(4π ε0 )/m5 (z7[t]-z5[t]))/Sqrt[((x7[t]-x5[t])^2+(y7[t]-y5[t])^2+(z7[t]-z5[t])^2)^3]+
(-q5*q8/(4π ε0 )/m5 (z8[t]-z5[t]))/Sqrt[((x8[t]-x5[t])^2+(y8[t]-y5[t])^2+(z8[t]-z5[t])^2)^3]+
(-q5*q9/(4π ε0 )/m5 (z9[t]-z5[t]))/Sqrt[((x9[t]-x5[t])^2+(y9[t]-y5[t])^2+(z9[t]-z5[t])^2)^3]+
(-q5*q0/(4π ε0 )/m5 (z0[t]-z5[t]))/Sqrt[((x0[t]-x5[t])^2+(y0[t]-y5[t])^2+(z0[t]-z5[t])^2)^3]],
vx6'[t] ==
(G m1 (x1[t]-x6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(G m2 (x2[t]-x6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(G m3 (x3[t]-x6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(G m4 (x4[t]-x6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(G m5 (x5[t]-x6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(G m7 (x7[t]-x6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(G m8 (x8[t]-x6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(G m9 (x9[t]-x6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(G m0 (x0[t]-x6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]+
If[q6 == 0, 0,
(-q6*q1/(4π ε0 )/m6 (x1[t]-x6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(-q6*q2/(4π ε0 )/m6 (x2[t]-x6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(-q6*q3/(4π ε0 )/m6 (x3[t]-x6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(-q6*q4/(4π ε0 )/m6 (x4[t]-x6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(-q6*q5/(4π ε0 )/m6 (x5[t]-x6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(-q6*q7/(4π ε0 )/m6 (x7[t]-x6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(-q6*q8/(4π ε0 )/m6 (x8[t]-x6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(-q6*q9/(4π ε0 )/m6 (x9[t]-x6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(-q6*q0/(4π ε0 )/m6 (x0[t]-x6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]],
vy6'[t] ==
(G m1 (y1[t]-y6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(G m2 (y2[t]-y6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(G m3 (y3[t]-y6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(G m4 (y4[t]-y6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(G m5 (y5[t]-y6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(G m7 (y7[t]-y6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(G m8 (y8[t]-y6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(G m9 (y9[t]-y6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(G m0 (y0[t]-y6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]+
If[q6 == 0, 0,
(-q6*q1/(4π ε0 )/m6 (y1[t]-y6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(-q6*q2/(4π ε0 )/m6 (y2[t]-y6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(-q6*q3/(4π ε0 )/m6 (y3[t]-y6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(-q6*q4/(4π ε0 )/m6 (y4[t]-y6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(-q6*q5/(4π ε0 )/m6 (y5[t]-y6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(-q6*q7/(4π ε0 )/m6 (y7[t]-y6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(-q6*q8/(4π ε0 )/m6 (y8[t]-y6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(-q6*q9/(4π ε0 )/m6 (y9[t]-y6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(-q6*q0/(4π ε0 )/m6 (y0[t]-y6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]],
vz6'[t] ==
(G m1 (z1[t]-z6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(G m2 (z2[t]-z6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(G m3 (z3[t]-z6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(G m4 (z4[t]-z6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(G m5 (z5[t]-z6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(G m7 (z7[t]-z6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(G m8 (z8[t]-z6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(G m9 (z9[t]-z6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(G m0 (z0[t]-z6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]+
If[q6 == 0, 0,
(-q6*q1/(4π ε0 )/m6 (z1[t]-z6[t]))/Sqrt[((x1[t]-x6[t])^2+(y1[t]-y6[t])^2+(z1[t]-z6[t])^2)^3]+
(-q6*q2/(4π ε0 )/m6 (z2[t]-z6[t]))/Sqrt[((x2[t]-x6[t])^2+(y2[t]-y6[t])^2+(z2[t]-z6[t])^2)^3]+
(-q6*q3/(4π ε0 )/m6 (z3[t]-z6[t]))/Sqrt[((x3[t]-x6[t])^2+(y3[t]-y6[t])^2+(z3[t]-z6[t])^2)^3]+
(-q6*q4/(4π ε0 )/m6 (z4[t]-z6[t]))/Sqrt[((x4[t]-x6[t])^2+(y4[t]-y6[t])^2+(z4[t]-z6[t])^2)^3]+
(-q6*q5/(4π ε0 )/m6 (z5[t]-z6[t]))/Sqrt[((x5[t]-x6[t])^2+(y5[t]-y6[t])^2+(z5[t]-z6[t])^2)^3]+
(-q6*q7/(4π ε0 )/m6 (z7[t]-z6[t]))/Sqrt[((x7[t]-x6[t])^2+(y7[t]-y6[t])^2+(z7[t]-z6[t])^2)^3]+
(-q6*q8/(4π ε0 )/m6 (z8[t]-z6[t]))/Sqrt[((x8[t]-x6[t])^2+(y8[t]-y6[t])^2+(z8[t]-z6[t])^2)^3]+
(-q6*q9/(4π ε0 )/m6 (z9[t]-z6[t]))/Sqrt[((x9[t]-x6[t])^2+(y9[t]-y6[t])^2+(z9[t]-z6[t])^2)^3]+
(-q6*q0/(4π ε0 )/m6 (z0[t]-z6[t]))/Sqrt[((x0[t]-x6[t])^2+(y0[t]-y6[t])^2+(z0[t]-z6[t])^2)^3]],
vx7'[t] ==
(G m1 (x1[t]-x7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(G m2 (x2[t]-x7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(G m3 (x3[t]-x7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(G m4 (x4[t]-x7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(G m5 (x5[t]-x7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(G m6 (x6[t]-x7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(G m8 (x8[t]-x7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(G m9 (x9[t]-x7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(G m0 (x0[t]-x7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]+
If[q7 == 0, 0,
(-q7*q1/(4π ε0 )/m7 (x1[t]-x7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(-q7*q2/(4π ε0 )/m7 (x2[t]-x7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(-q7*q3/(4π ε0 )/m7 (x3[t]-x7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(-q7*q4/(4π ε0 )/m7 (x4[t]-x7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(-q7*q5/(4π ε0 )/m7 (x5[t]-x7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(-q7*q6/(4π ε0 )/m7 (x6[t]-x7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(-q7*q8/(4π ε0 )/m7 (x8[t]-x7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(-q7*q9/(4π ε0 )/m7 (x9[t]-x7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(-q7*q0/(4π ε0 )/m7 (x0[t]-x7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]],
vy7'[t] ==
(G m1 (y1[t]-y7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(G m2 (y2[t]-y7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(G m3 (y3[t]-y7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(G m4 (y4[t]-y7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(G m5 (y5[t]-y7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(G m6 (y6[t]-y7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(G m8 (y8[t]-y7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(G m9 (y9[t]-y7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(G m0 (y0[t]-y7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]+
If[q7 == 0, 0,
(-q7*q1/(4π ε0 )/m7 (y1[t]-y7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(-q7*q2/(4π ε0 )/m7 (y2[t]-y7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(-q7*q3/(4π ε0 )/m7 (y3[t]-y7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(-q7*q4/(4π ε0 )/m7 (y4[t]-y7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(-q7*q5/(4π ε0 )/m7 (y5[t]-y7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(-q7*q6/(4π ε0 )/m7 (y6[t]-y7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(-q7*q8/(4π ε0 )/m7 (y8[t]-y7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(-q7*q9/(4π ε0 )/m7 (y9[t]-y7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(-q7*q0/(4π ε0 )/m7 (y0[t]-y7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]],
vz7'[t] ==
(G m1 (z1[t]-z7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(G m2 (z2[t]-z7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(G m3 (z3[t]-z7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(G m4 (z4[t]-z7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(G m5 (z5[t]-z7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(G m6 (z6[t]-z7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(G m8 (z8[t]-z7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(G m9 (z9[t]-z7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(G m0 (z0[t]-z7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]+
If[q7 == 0, 0,
(-q7*q1/(4π ε0 )/m7 (z1[t]-z7[t]))/Sqrt[((x1[t]-x7[t])^2+(y1[t]-y7[t])^2+(z1[t]-z7[t])^2)^3]+
(-q7*q2/(4π ε0 )/m7 (z2[t]-z7[t]))/Sqrt[((x2[t]-x7[t])^2+(y2[t]-y7[t])^2+(z2[t]-z7[t])^2)^3]+
(-q7*q3/(4π ε0 )/m7 (z3[t]-z7[t]))/Sqrt[((x3[t]-x7[t])^2+(y3[t]-y7[t])^2+(z3[t]-z7[t])^2)^3]+
(-q7*q4/(4π ε0 )/m7 (z4[t]-z7[t]))/Sqrt[((x4[t]-x7[t])^2+(y4[t]-y7[t])^2+(z4[t]-z7[t])^2)^3]+
(-q7*q5/(4π ε0 )/m7 (z5[t]-z7[t]))/Sqrt[((x5[t]-x7[t])^2+(y5[t]-y7[t])^2+(z5[t]-z7[t])^2)^3]+
(-q7*q6/(4π ε0 )/m7 (z6[t]-z7[t]))/Sqrt[((x6[t]-x7[t])^2+(y6[t]-y7[t])^2+(z6[t]-z7[t])^2)^3]+
(-q7*q8/(4π ε0 )/m7 (z8[t]-z7[t]))/Sqrt[((x8[t]-x7[t])^2+(y8[t]-y7[t])^2+(z8[t]-z7[t])^2)^3]+
(-q7*q9/(4π ε0 )/m7 (z9[t]-z7[t]))/Sqrt[((x9[t]-x7[t])^2+(y9[t]-y7[t])^2+(z9[t]-z7[t])^2)^3]+
(-q7*q0/(4π ε0 )/m7 (z0[t]-z7[t]))/Sqrt[((x0[t]-x7[t])^2+(y0[t]-y7[t])^2+(z0[t]-z7[t])^2)^3]],
vx8'[t] ==
(G m1 (x1[t]-x8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(G m2 (x2[t]-x8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(G m3 (x3[t]-x8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(G m4 (x4[t]-x8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(G m5 (x5[t]-x8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(G m6 (x6[t]-x8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(G m7 (x7[t]-x8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(G m9 (x9[t]-x8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(G m0 (x0[t]-x8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]+
If[q8 == 0, 0,
(-q8*q1/(4π ε0 )/m8 (x1[t]-x8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(-q8*q2/(4π ε0 )/m8 (x2[t]-x8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(-q8*q3/(4π ε0 )/m8 (x3[t]-x8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(-q8*q4/(4π ε0 )/m8 (x4[t]-x8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(-q8*q5/(4π ε0 )/m8 (x5[t]-x8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(-q8*q6/(4π ε0 )/m8 (x6[t]-x8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(-q8*q7/(4π ε0 )/m8 (x7[t]-x8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(-q8*q9/(4π ε0 )/m8 (x9[t]-x8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(-q8*q0/(4π ε0 )/m8 (x0[t]-x8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]],
vy8'[t] ==
(G m1 (y1[t]-y8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(G m2 (y2[t]-y8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(G m3 (y3[t]-y8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(G m4 (y4[t]-y8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(G m5 (y5[t]-y8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(G m6 (y6[t]-y8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(G m7 (y7[t]-y8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(G m9 (y9[t]-y8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(G m0 (y0[t]-y8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]+
If[q8 == 0, 0,
(-q8*q1/(4π ε0 )/m8 (y1[t]-y8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(-q8*q2/(4π ε0 )/m8 (y2[t]-y8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(-q8*q3/(4π ε0 )/m8 (y3[t]-y8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(-q8*q4/(4π ε0 )/m8 (y4[t]-y8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(-q8*q5/(4π ε0 )/m8 (y5[t]-y8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(-q8*q6/(4π ε0 )/m8 (y6[t]-y8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(-q8*q7/(4π ε0 )/m8 (y7[t]-y8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(-q8*q9/(4π ε0 )/m8 (y9[t]-y8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(-q8*q0/(4π ε0 )/m8 (y0[t]-y8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]],
vz8'[t] ==
(G m1 (z1[t]-z8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(G m2 (z2[t]-z8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(G m3 (z3[t]-z8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(G m4 (z4[t]-z8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(G m5 (z5[t]-z8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(G m6 (z6[t]-z8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(G m7 (z7[t]-z8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(G m9 (z9[t]-z8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(G m0 (z0[t]-z8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]+
If[q8 == 0, 0,
(-q8*q1/(4π ε0 )/m8 (z1[t]-z8[t]))/Sqrt[((x1[t]-x8[t])^2+(y1[t]-y8[t])^2+(z1[t]-z8[t])^2)^3]+
(-q8*q2/(4π ε0 )/m8 (z2[t]-z8[t]))/Sqrt[((x2[t]-x8[t])^2+(y2[t]-y8[t])^2+(z2[t]-z8[t])^2)^3]+
(-q8*q3/(4π ε0 )/m8 (z3[t]-z8[t]))/Sqrt[((x3[t]-x8[t])^2+(y3[t]-y8[t])^2+(z3[t]-z8[t])^2)^3]+
(-q8*q4/(4π ε0 )/m8 (z4[t]-z8[t]))/Sqrt[((x4[t]-x8[t])^2+(y4[t]-y8[t])^2+(z4[t]-z8[t])^2)^3]+
(-q8*q5/(4π ε0 )/m8 (z5[t]-z8[t]))/Sqrt[((x5[t]-x8[t])^2+(y5[t]-y8[t])^2+(z5[t]-z8[t])^2)^3]+
(-q8*q6/(4π ε0 )/m8 (z6[t]-z8[t]))/Sqrt[((x6[t]-x8[t])^2+(y6[t]-y8[t])^2+(z6[t]-z8[t])^2)^3]+
(-q8*q7/(4π ε0 )/m8 (z7[t]-z8[t]))/Sqrt[((x7[t]-x8[t])^2+(y7[t]-y8[t])^2+(z7[t]-z8[t])^2)^3]+
(-q8*q9/(4π ε0 )/m8 (z9[t]-z8[t]))/Sqrt[((x9[t]-x8[t])^2+(y9[t]-y8[t])^2+(z9[t]-z8[t])^2)^3]+
(-q8*q0/(4π ε0 )/m8 (z0[t]-z8[t]))/Sqrt[((x0[t]-x8[t])^2+(y0[t]-y8[t])^2+(z0[t]-z8[t])^2)^3]],
vx9'[t] ==
(G m1 (x1[t]-x9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(G m2 (x2[t]-x9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(G m3 (x3[t]-x9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(G m4 (x4[t]-x9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(G m5 (x5[t]-x9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(G m6 (x6[t]-x9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(G m7 (x7[t]-x9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(G m8 (x8[t]-x9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(G m0 (x0[t]-x9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]+
If[q9 == 0, 0,
(-q9*q1/(4π ε0 )/m9 (x1[t]-x9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(-q9*q2/(4π ε0 )/m9 (x2[t]-x9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(-q9*q3/(4π ε0 )/m9 (x3[t]-x9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(-q9*q4/(4π ε0 )/m9 (x4[t]-x9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(-q9*q5/(4π ε0 )/m9 (x5[t]-x9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(-q9*q6/(4π ε0 )/m9 (x6[t]-x9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(-q9*q7/(4π ε0 )/m9 (x7[t]-x9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(-q9*q8/(4π ε0 )/m9 (x8[t]-x9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(-q9*q0/(4π ε0 )/m9 (x0[t]-x9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]],
vy9'[t] ==
(G m1 (y1[t]-y9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(G m2 (y2[t]-y9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(G m3 (y3[t]-y9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(G m4 (y4[t]-y9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(G m5 (y5[t]-y9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(G m6 (y6[t]-y9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(G m7 (y7[t]-y9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(G m8 (y8[t]-y9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(G m0 (y0[t]-y9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]+
If[q9 == 0, 0,
(-q9*q1/(4π ε0 )/m9 (y1[t]-y9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(-q9*q2/(4π ε0 )/m9 (y2[t]-y9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(-q9*q3/(4π ε0 )/m9 (y3[t]-y9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(-q9*q4/(4π ε0 )/m9 (y4[t]-y9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(-q9*q5/(4π ε0 )/m9 (y5[t]-y9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(-q9*q6/(4π ε0 )/m9 (y6[t]-y9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(-q9*q7/(4π ε0 )/m9 (y7[t]-y9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(-q9*q8/(4π ε0 )/m9 (y8[t]-y9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(-q9*q0/(4π ε0 )/m9 (y0[t]-y9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]],
vz9'[t] ==
(G m1 (z1[t]-z9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(G m2 (z2[t]-z9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(G m3 (z3[t]-z9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(G m4 (z4[t]-z9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(G m5 (z5[t]-z9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(G m6 (z6[t]-z9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(G m7 (z7[t]-z9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(G m8 (z8[t]-z9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(G m0 (z0[t]-z9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]+
If[q9 == 0, 0,
(-q9*q1/(4π ε0 )/m9 (z1[t]-z9[t]))/Sqrt[((x1[t]-x9[t])^2+(y1[t]-y9[t])^2+(z1[t]-z9[t])^2)^3]+
(-q9*q2/(4π ε0 )/m9 (z2[t]-z9[t]))/Sqrt[((x2[t]-x9[t])^2+(y2[t]-y9[t])^2+(z2[t]-z9[t])^2)^3]+
(-q9*q3/(4π ε0 )/m9 (z3[t]-z9[t]))/Sqrt[((x3[t]-x9[t])^2+(y3[t]-y9[t])^2+(z3[t]-z9[t])^2)^3]+
(-q9*q4/(4π ε0 )/m9 (z4[t]-z9[t]))/Sqrt[((x4[t]-x9[t])^2+(y4[t]-y9[t])^2+(z4[t]-z9[t])^2)^3]+
(-q9*q5/(4π ε0 )/m9 (z5[t]-z9[t]))/Sqrt[((x5[t]-x9[t])^2+(y5[t]-y9[t])^2+(z5[t]-z9[t])^2)^3]+
(-q9*q6/(4π ε0 )/m9 (z6[t]-z9[t]))/Sqrt[((x6[t]-x9[t])^2+(y6[t]-y9[t])^2+(z6[t]-z9[t])^2)^3]+
(-q9*q7/(4π ε0 )/m9 (z7[t]-z9[t]))/Sqrt[((x7[t]-x9[t])^2+(y7[t]-y9[t])^2+(z7[t]-z9[t])^2)^3]+
(-q9*q8/(4π ε0 )/m9 (z8[t]-z9[t]))/Sqrt[((x8[t]-x9[t])^2+(y8[t]-y9[t])^2+(z8[t]-z9[t])^2)^3]+
(-q9*q0/(4π ε0 )/m9 (z0[t]-z9[t]))/Sqrt[((x0[t]-x9[t])^2+(y0[t]-y9[t])^2+(z0[t]-z9[t])^2)^3]],
vx0'[t] ==
(G m1 (x1[t]-x0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(G m2 (x2[t]-x0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(G m3 (x3[t]-x0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(G m4 (x4[t]-x0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(G m5 (x5[t]-x0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(G m6 (x6[t]-x0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(G m7 (x7[t]-x0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(G m8 (x8[t]-x0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(G m9 (x9[t]-x0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]+
If[q0 == 0, 0,
(-q0*q1/(4π ε0 )/m0 (x1[t]-x0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(-q0*q2/(4π ε0 )/m0 (x2[t]-x0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(-q0*q3/(4π ε0 )/m0 (x3[t]-x0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(-q0*q4/(4π ε0 )/m0 (x4[t]-x0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(-q0*q5/(4π ε0 )/m0 (x5[t]-x0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(-q0*q6/(4π ε0 )/m0 (x6[t]-x0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(-q0*q7/(4π ε0 )/m0 (x7[t]-x0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(-q0*q8/(4π ε0 )/m0 (x8[t]-x0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(-q0*q9/(4π ε0 )/m0 (x9[t]-x0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]],
vy0'[t] ==
(G m1 (y1[t]-y0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(G m2 (y2[t]-y0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(G m3 (y3[t]-y0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(G m4 (y4[t]-y0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(G m5 (y5[t]-y0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(G m6 (y6[t]-y0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(G m7 (y7[t]-y0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(G m8 (y8[t]-y0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(G m9 (y9[t]-y0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]+
If[q0 == 0, 0,
(-q0*q1/(4π ε0 )/m0 (y1[t]-y0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(-q0*q2/(4π ε0 )/m0 (y2[t]-y0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(-q0*q3/(4π ε0 )/m0 (y3[t]-y0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(-q0*q4/(4π ε0 )/m0 (y4[t]-y0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(-q0*q5/(4π ε0 )/m0 (y5[t]-y0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(-q0*q6/(4π ε0 )/m0 (y6[t]-y0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(-q0*q7/(4π ε0 )/m0 (y7[t]-y0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(-q0*q8/(4π ε0 )/m0 (y8[t]-y0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(-q0*q9/(4π ε0 )/m0 (y9[t]-y0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]],
vz0'[t] ==
(G m1 (z1[t]-z0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(G m2 (z2[t]-z0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(G m3 (z3[t]-z0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(G m4 (z4[t]-z0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(G m5 (z5[t]-z0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(G m6 (z6[t]-z0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(G m7 (z7[t]-z0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(G m8 (z8[t]-z0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(G m9 (z9[t]-z0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]+
If[q0 == 0, 0,
(-q0*q1/(4π ε0 )/m0 (z1[t]-z0[t]))/Sqrt[((x1[t]-x0[t])^2+(y1[t]-y0[t])^2+(z1[t]-z0[t])^2)^3]+
(-q0*q2/(4π ε0 )/m0 (z2[t]-z0[t]))/Sqrt[((x2[t]-x0[t])^2+(y2[t]-y0[t])^2+(z2[t]-z0[t])^2)^3]+
(-q0*q3/(4π ε0 )/m0 (z3[t]-z0[t]))/Sqrt[((x3[t]-x0[t])^2+(y3[t]-y0[t])^2+(z3[t]-z0[t])^2)^3]+
(-q0*q4/(4π ε0 )/m0 (z4[t]-z0[t]))/Sqrt[((x4[t]-x0[t])^2+(y4[t]-y0[t])^2+(z4[t]-z0[t])^2)^3]+
(-q0*q5/(4π ε0 )/m0 (z5[t]-z0[t]))/Sqrt[((x5[t]-x0[t])^2+(y5[t]-y0[t])^2+(z5[t]-z0[t])^2)^3]+
(-q0*q6/(4π ε0 )/m0 (z6[t]-z0[t]))/Sqrt[((x6[t]-x0[t])^2+(y6[t]-y0[t])^2+(z6[t]-z0[t])^2)^3]+
(-q0*q7/(4π ε0 )/m0 (z7[t]-z0[t]))/Sqrt[((x7[t]-x0[t])^2+(y7[t]-y0[t])^2+(z7[t]-z0[t])^2)^3]+
(-q0*q8/(4π ε0 )/m0 (z8[t]-z0[t]))/Sqrt[((x8[t]-x0[t])^2+(y8[t]-y0[t])^2+(z8[t]-z0[t])^2)^3]+
(-q0*q9/(4π ε0 )/m0 (z9[t]-z0[t]))/Sqrt[((x9[t]-x0[t])^2+(y9[t]-y0[t])^2+(z9[t]-z0[t])^2)^3]],
x1[0] == x1x, y1[0] == y1y, z1[0] == z1z,
x2[0] == x2x, y2[0] == y2y, z2[0] == z2z,
x3[0] == x3x, y3[0] == y3y, z3[0] == z3z,
x4[0] == x4x, y4[0] == y4y, z4[0] == z4z,
x5[0] == x5x, y5[0] == y5y, z5[0] == z5z,
x6[0] == x6x, y6[0] == y6y, z6[0] == z6z,
x7[0] == x7x, y7[0] == y7y, z7[0] == z7z,
x8[0] == x8x, y8[0] == y8y, z8[0] == z8z,
x9[0] == x9x, y9[0] == y9y, z9[0] == z9z,
x0[0] == x0x, y0[0] == y0y, z0[0] == z0z,
vx1[0] == v1x, vy1[0] == v1y, vz1[0] == v1z,
vx2[0] == v2x, vy2[0] == v2y, vz2[0] == v2z,
vx3[0] == v3x, vy3[0] == v3y, vz3[0] == v3z,
vx4[0] == v4x, vy4[0] == v4y, vz4[0] == v4z,
vx5[0] == v5x, vy5[0] == v5y, vz5[0] == v5z,
vx6[0] == v6x, vy6[0] == v6y, vz6[0] == v6z,
vx7[0] == v7x, vy7[0] == v7y, vz7[0] == v7z,
vx8[0] == v8x, vy8[0] == v8y, vz8[0] == v8z,
vx9[0] == v9x, vy9[0] == v9y, vz9[0] == v9z,
vx0[0] == v0x, vy0[0] == v0y, vz0[0] == v0z},
{x1, x2, x3, x4, x5, x6, x7, x8, x9, x0, y1, y2, y3, y4, y5, y6, y7, y8, y9, y0, z1, z2, z3, z4, z5, z6, z7, z8, z9, z0,
vx1, vx2, vx3, vx4, vx5, vx6, vx7, vx8, vx9, vx0, vy1, vy2, vy3, vy4, vy5, vy6, vy7, vy8, vy9, vy0, vz1, vz2, vz3, vz4, vz5, vz6, vz7, vz8, vz9, vz0},
{t, 0, T0},
WorkingPrecision-> wp,
MaxSteps-> Infinity,
Method-> mta,
InterpolationOrder-> All,
StepMonitor :> (laststep=plunge; plunge=t;
stepsize=plunge-laststep;), Method->{"EventLocator",
"Event" :> (If[stepsize<1*^-4, 0, 1])}];
(* Position, Geschwindigkeit *)
f2p[t_]={{x1[t], y1[t], z1[t]}, {x2[t], y2[t], z2[t]}, {x3[t], y3[t], z3[t]}, {x4[t], y4[t], z4[t]}, {x5[t], y5[t], z5[t]}, {x6[t], y6[t], z6[t]}, {x7[t], y7[t], z7[t]}, {x8[t], y8[t], z8[t]}, {x9[t], y9[t], z9[t]}, {x0[t], y0[t], z0[t]}}/.nds[[1]];
f2v[t_]={{vx1[t], vy1[t], vz1[t]}, {vx2[t], vy2[t], vz2[t]}, {vx3[t], vy3[t], vz3[t]}, {vx4[t], vy4[t], vz4[t]}, {vx5[t], vy5[t], vz5[t]}, {vx6[t], vy6[t], vz6[t]}, {vx7[t], vy7[t], vz7[t]}, {vx8[t], vy8[t], vz8[t]}, {vx9[t], vy9[t], vz9[t]}, {vx0[t], vy0[t], vz0[t]}}/.nds[[1]];
swp[t_]=(m1 Evaluate[f2p[t][[1]]]+m2 Evaluate[f2p[t][[2]]]+m3 Evaluate[f2p[t][[3]]]+m4 Evaluate[f2p[t][[4]]]+m5 Evaluate[f2p[t][[5]]]+m6 Evaluate[f2p[t][[6]]]+m7 Evaluate[f2p[t][[7]]]+m8 Evaluate[f2p[t][[8]]]+m9 Evaluate[f2p[t][[9]]]+m0 Evaluate[f2p[t][[10]]])/(m1+m2+m3+m4+m5+m6+m7+m8+m9+m0);
(* Merkurjahr *)
ym = 87969/1000 dy;
(* Funktionen *)
w[n_, t_] := ArcTan[f2p[t][[n, 1]]-f2p[t][[1, 1]], f2p[t][[n, 2]]-f2p[t][[1, 2]]]
r[n_, t_] := Norm[f2p[t][[n]]-f2p[t][[1]]]
μ[n_, t_] := Quiet[τ/.FindMinimum[r[n, τ], {τ, t}][[2]]]
t1 = Quiet[μ[2, T1]]; "t1" -> t1/yr "years"
t2 = Quiet[μ[2, T2]]; "t2" -> t2/yr "years"
Δt = t2-t1; "Δt" -> Δt/yr "yr"
(* neutonischer Shift *)
Δα = (w[2, t2]-w[2, t1]);
ΔΑ = Δα*3600*180/π/Δt*100 yr;
"Δα" -> ΔΑ "arcsec per 100 years"Output:
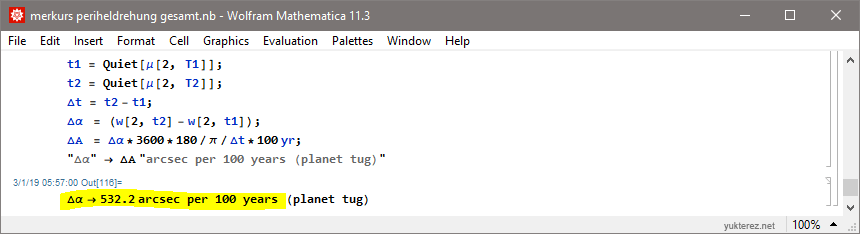

2) Einstein (gravitoelektrischer Effekt)

Input:
Code: Alles auswählen
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* ||| Mathematica Syntax || yukterez.net || Perihelionshift, Relativistic Weak Field ||| *)
(* |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| *)
(* große Halbachse, Exzentrizität, Umlaufperiode *)
a = 0.387099273 Au;
e = 0.205635934;
Δt = ym;
(* gravitoelektrischer Shift *)
Δβ = (24 π^3 a^2)/(Δt^2 c^2 (1-e^2));
ΔΒ = Δβ*3600*180/π/Δt*100yr;
"Δβ" -> ΔΒ "arcsec per 100 years"Output:
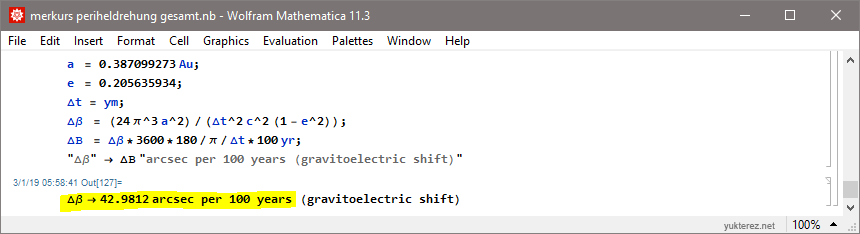

3) Summe (neutonischer und einsteinscher Anteil addiert)

4) Vergleich mit der Literatur:

5) Text (Lorem ipsum)

Hier werden die Ephemeriden von 2019 in der Zeit zurückintegriert. Berücksichtigt sind alle Planeten inklusive Pluto/Charon und die Reflexbewegung der Sonne um das Baryzentrum des Sonnensystems, der Einfluss von Asteroiden und Planetoiden wurde vernachlässigt (diese tragen ca. 0.13"/Jahrhundert bei). Die Startpositionen und Geschwindigkeiten der Planeten wurden von JPL übernommen, und ihre Massen von Wolframalpha. Je nach Quelle können die Massen der Planeten an den hinteren Kommastellen auch etwas von den hier verwendeten Zahlen abweichen. Wenn man es ganz genau will kann man statt der Planetenmasse die Masse der Planeten samt ihrer Monde eingeben, wofür ich hier da das Ergebnis auch so ganz gut passt zu faul war. Arbeitsblatt: merkurs.periheldrehung.nb, all in 1 Code: controlc.com/cf7be975

6) Mathematik (Newton und Einstein)

Bewegungsgleichung für die Mehrkörpersimulation des Sonnensystems:
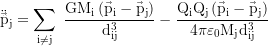
wobei der zweite Term aufgrund der elektrischen Neutralität wegfällt. Dabei ist
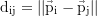
der Abstand zwischen Körper i und j. Die azimutale Winkelkoordinate des Merkur relativ zur Sonne ist
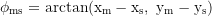
mit dem Subscript m für Merkur und s für die Sonne. Nun wird numerisch nach der Zeit des Perigäums
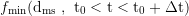
gesolved. t₀ bis t₀+Δt ist dabei die Zeitspanne in der nach der nächsten Annäherung gesucht wird, wobei Δt Merkurs Umlaufperiode ist. Vergleicht man nun zwei Φms die sich zu den Minima von dms gehörigen t bei unterschiedlichen t₀ ergeben erhält man die sich aus der Wechselwirkung mit den anderen Planeten ergebende Periheldrehung innerhalb des jeweiligen Zeitrahmens. Der gravitoelektrische Shift pro Umlaufperiode ist
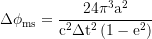
wobei a die große Halbachse und e die Exzentrizität des Merkur ist. Die gravitoelektrische Formel funktioniert nur im schwachen Feld, für die Rechnung die auch im starken Feld gilt siehe hier.







